Cargas horizontal e vertical e um momento são aplicados à uma estrutura em balanço de comprimento , como mostrado na figura abaixo.
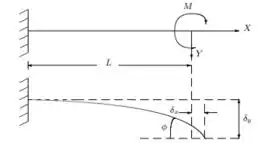
Na extremidade livre, o alongamento , a deflexão e o giro (igual ao ângulo com a horizontal) são relacionados com as cargas, da seguinte maneira:
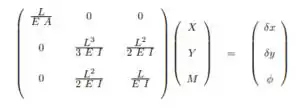
onde:
• é o módulo de Young
• é a área de secção transversal
• é o momento de inércia
A matriz do sistema acima é positiva definida e é chamada matriz de flexibilidade da estrutura.
a) Obter a inversa da matriz de flexibilidade correspondente aos seguintes dados:
b) Usando o resultado obtido em a) calcular as cargas e o momento correspondentes a:
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de cálculo numérico de Franco e Neide dado as Cargas horizontal e vertical e um momento são aplicados à uma estrutura em balanço de comprimento , como mostrado na figura abaixo.
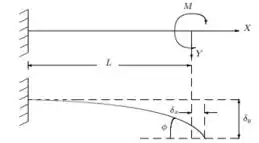
Na extremidade livre, o alongamento , a deflexão e o giro (igual ao ângulo com a horizontal) são relacionados com as cargas, da seguinte maneira:
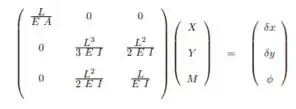
onde:
• é o módulo de Young
• é a área de secção transversal
• é o momento de inércia
A matriz do sistema acima é positiva definida e é chamada matriz de flexibilidade da estrutura.
a) Obter a inversa da matriz de flexibilidade correspondente aos seguintes dados:
b) Usando o resultado obtido em a) calcular as cargas e o momento correspondentes a:

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galera dado o modelo de uma deflexão de uma viga com sua forma expressa em um sistema como demonstrado no passo anterior temos que na letra (a) para se determinar a matriz flexibilidade temos que,
Ficando,
Já n letra (b) temos complementando a matriz (a) que,

Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.
Resposta
a)
b)