Zero da Função

Fala aí, você acaba de chegar no Responde Aí, a plataforma de exatas que vai salvar o seu semestre!

Nosso objetivo aqui hoje é bater um papo rápido sobre como encontra o zero de funções usando métodos de Cálculo Numérico!

Então pra começar com tudo, eu vou te perguntar! Como você faria para encontrar pelo menos um zero da função abaixo?

Meio complicado, certo!?

Uma forma de resolver esse problema é usando métodos interativos! Hoje eu vou te ensinar a resolver essa equação usando o Método da Bisseção. Mas um passo de cada vez, primeiro vamos entender direitinho o que é o zero da função!

O que é o zero de uma função?

Se liga aqui nesse gráfico de uma função qualquer:

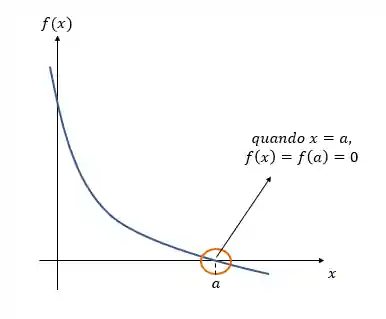
O zero da função, também chamado de raiz da função, é justamente aquele ponto que está marcado aí no gráfico, é o valor de que faz com que a função seja igual a . No caso da imagem acima, o zero da função é o ponto . Graficamente, o zero da função é o ponto em que a curva corta o eixo .

Na escola a gente aprende a achar a raiz, ou raízes da função analiticamente! Quando tínhamos um polinômio de primeiro grau era só igualar a função a zero, isolar o e pronto. Ou quando tínhamos uma função de segundo grau, usávamos a Fórmula de Bháskara. Bem assim:

Fazemos e usamos Bháskara:

Temos , e , substituindo:

E finalmente calculamos:

E pronto achamos os zeros da função!

Saudades desses tempos mais simples, não? 🥲🥲🥲

Mas calma, ninguém precisa chorar! O Responde Aí está aqui pra te ajudar! Até rimou! 🤣🤣🤣🤣

Vamos voltar ao nosso exemplo:

Nesses casos nós usaremos os métodos numéricos para calcular o zero das funções, mas especificamente o Método da Bissecção!

No vídeo a baixo a gente pode aprender juntinhos sobre esse método e como usa-lo pra resolver esse problema 👇👇👇

Existem um monte de outros métodos numéricos. Entre eles o método da posição falsa, do ponto fixo, Newton-Raphson e finalmente, o método da secante!

A ideia central desses métodos é a seguinte:

1. Definimos um intervalo que contenha o zero da função;
2. A partir desse intervalo fazemos uma aproximação inicial do valor do zero da função;
3. A partir da aproximação inicial nós vamos refinando o intervalo e fazendo novas aproximações. E esse processo é feito repetidas vezes em sequência.
4. Estipulamos um critério de parada e só paramos de repetir o processo quando o critério é satisfeito.

Mas não se esqueça, cada método tem seu jeitinho especial!

Quer entender melhor como empregamos e quais são os métodos para o cálculo de zero de funções? Se sim, é só continuar aqui com a gente do Responde Aí.

Aqui embaixo você vai encontrar o nosso Raio-X completíssimo com tudo que você precisa pra arrasar na sua prova! Dá uma conferida! 👇👇👇