Interpolação

Olá, se você chegou até aqui é porque está precisando aprender sobre Interpolação, então vamos logo para o que tanto te interessa haha

Imagina que estamos vendo um carro andando e queremos marcar a distância percorrida por esse carro a cada instante de tempo. Concorda comigo que podemos montar uma tabela assim:

e ir anotando o tempo e a distância percorrida em cada tempo?

Ao final nós teremos um conjunto de pontos .

Suponha que a gente fez essas marcações e nossa tabela ficou assim:

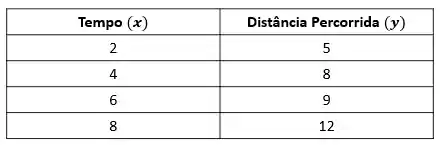
Se eu pergunto assim: Qual a distância percorrida no tempo ? Rapidinho a gente responde né? Foi . Mas se eu pergunto a distância percorrida no tempo ? Aí o bicho pega né haha

É aí que entra nosso assunto de hoje, a interpolação. Basicamente, todo conjunto de pontos pode ser aproximado por uma função. Na interpolação é justamente isso que vamos fazer, vamos pegar esse conjunto de pontos e aproximar ele por uma função.

A interpolação mais comum é a interpolação polinomial. Nessa interpolação nós vamos pegar o nosso conjunto de dados e aproximar ele por uma função polinomial. Mas como fazemos isso?

Vamos lá com um exemplo. Considere o conjunto de pontos abaixo:

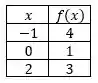
Para obtermos a interpolação polinomial desse conjunto vamos fazer o seguinte:

Como nós temos três pontos, a nossa função polinomial será de grau . Isso é regra tá bom? O grau na função de interpolação é sempre o número de pontos menos , beleza?

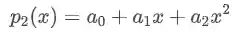
Agora o que temos que fazer é achar quem serão os coeficientes , e . Para isso vamos pegar cada ponto que temos e substituir eles nessa função , desse jeito aqui:

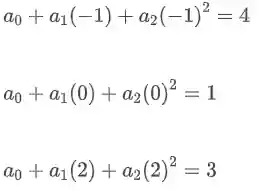
E notou que agora nós temos um sitema linear pra resolver? E é isso que vamos fazer agora, resolver o sistema linear e achar os coeficientes:

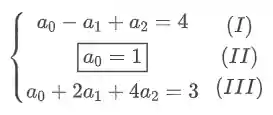
Substituindo na equação :

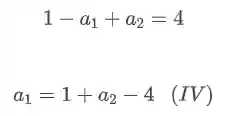
Agora substituindo e a expressão para na equação :

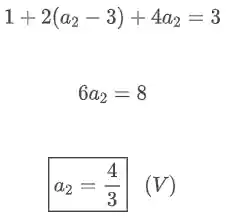
E por último, vamos substituir na equação :

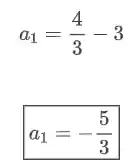
E assim, temos que:

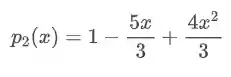
E é assim que fazemos uma interpolação polinomial. Tranquilo não é?

Vou deixar logo aqui em seguida um vídeo sobre essa introdução rápida de interpolação, feito pela equipe incrível do Responde Aí:

Agora que você já viu essa introdução rapidinha você já está preparado para continuar e aprender tudo sobre interpolação. Aqui no Responde Aí nós temos todo esse conteúdo que você precisa, dá uma olhada no nosso Raio-X aqui embaixo 👇🏽 e veja tudo que nós podemos te oferecer 😉