Considere o circuito da figura a seguir, com resistências e baterias tal como indicado; escolhemos arbitrariamente as orientações das correntes.
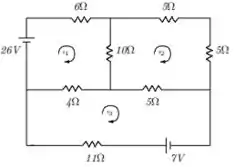
Aplicando a lei de Kirchoff, que diz que a soma algébrica das diferenças de potencial em qualquer circuito fechado ´e zero, achamos para as correntes :
a) E possível aplicar ao sistema acima o método de Gauss - Seidel com convergência assegurada?
b) Se possível, obtenha a solução com erro relativo
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de cálculo numérico de Franco e Neide ao considerarmos o circuito da figura a seguir, com resistências e baterias tal como indicado; escolhemos arbitrariamente as orientações das correntes.
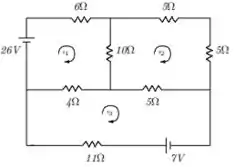
Aplicando a lei de Kirchoff, que diz que a soma algébrica das diferenças de potencial em qualquer circuito fechado ´e zero, achamos para as correntes :
a) E possível aplicar ao sistema acima o método de Gauss - Seidel com convergência assegurada?
b) Se possível, obtenha a solução com erro relativo

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galerinha dada o sistema das leis de Kirchoff representada por,
Temos que na letra (a) para o método de Gauss-Seidel com convergência assegurada, temos
Ficando,
Logo temos,
Já na letra (b) para se obter o erro relativo , temos
Logo ela obedece ao erro relativo.
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta
a)
b) obedece ao erro relativo.