Considere a malha quadrada da figura a seguir, cujos bordos são mantidos à temperatura de , o bordo à , com o uso de isolantes térmicos em
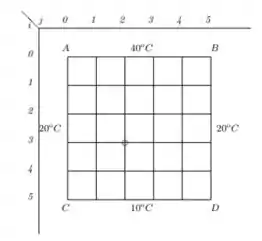
Para determinar as temperaturas de pontos interiores da malha, pode-se supor que a temperatura em cada ponto é igual à média aritmética dos quatro pontos contíguos. Por exemplo:
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de cálculo numérico de Franco e Neide considerando a malha quadrada da figura a seguir, cujos bordos são mantidos à temperatura de , o bordo à , com o uso de isolantes térmicos em
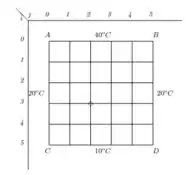
Para determinar as temperaturas de pontos interiores da malha, pode-se supor que a temperatura em cada ponto é igual à média aritmética dos quatro pontos contíguos. Por exemplo:

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galera dado no enunciado que os trechos,
Como é demonstrada na imagem do passo anterior, temos que para determinar a temperatura dos pontos anteriores vamos ter que,
Ficando,
Sendo as 16 equações com temperatura de
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta
as 16 equações com temperatura de