Considere o sistema linear do exercício anterior com . A aplicação do método de Jacobi fornece a tabela:
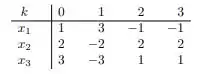
Existe alguma contradição com o exercício anterior? Você saberia explicar porque o método de Jacobi convergiu.
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de cálculo numérico de Franco e Neide considerando o sistema linear do exercício anterior com . A aplicação do método de Jacobi fornece a tabela:
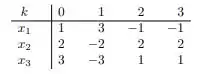
Existe alguma contradição com o exercício anterior? Você saberia explicar porque o método de Jacobi convergiu.

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galerinha nessa questão ele deseja determinar o sistema linear com base nos dados fornecidos por,
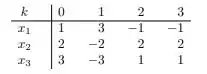
Com,
Temos,
Ficando,

Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.
Resposta