Determine as constantes a, b, c e d que produzirão uma fórmula de quadratura
que tem grau de precisão 4.
Passo 1
Bora pra ultima?
Simboráa
Considerando a fórmula de quadratura fornecida no enunciado.
Para determinar as constantes a, b, c e d exigimos quatro condições, portanto, suponha que a formula dada tenha precisão de grau3. Ou seja, é exato para .
Passo 2
Agora para k=0, tomar
Então de (1), LHS =
E
Como LRH= RSH iremos obter,
Passo 3
Agora para k=1, tomar
Então de (1), LHS =
E
Como LRH= RSH iremos obter,
Passo 4
Agora para k=2, tomar
Então de (1), LHS =
E
Como LRH= RSH iremos obter,
Agora para k=3, tomar
Então de (1), LHS =
E
Como LRH= RSH iremos obter,
Passo 5
Agora para k=4, tomar
Então de (1), LHS =
E
Como LRH= RSH iremos obter,
Passo 6
Resolvendo o sistema de equações temos
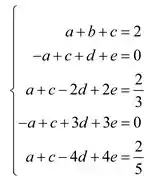
Usando o maple para resolver as equações acima
Entrada
![]()
Saída
![]()
Resposta
Os valores exigidos são