Elabore um algoritmo que tendo como dados n, a matriz onde é tal que para , e é um vetor , determina a solução do sistema linear pelo método de Eliminação de Gauss adaptado para sistemas tridiagonais.
a) Teste seu algoritmo para resolver o sistema dado por:
para vários valores de , e compare sua solução com a solução matemática:
Considere e tome em ambos os casos .
b) Teste seu algoritmo para resolver o sistema , onde:
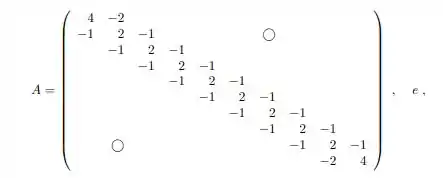
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de cálculo numérico de Franco e Neide elaborando um algoritmo que tendo como dados n, a matriz onde é tal que para , e é um vetor , determina a solução do sistema linear pelo método de Eliminação de Gauss adaptado para sistemas tridiagonais.
a) Teste seu algoritmo para resolver o sistema dado por:
para vários valores de , e compare sua solução com a solução matemática:
Considere e tome em ambos os casos .
b) Teste seu algoritmo para resolver o sistema , onde:
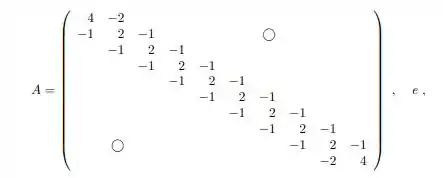

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galerinha na letra (a) ele pede testar o algoritmo tendo sido dado,
Com,
Tendo que considerar para
Para temos
Para ,
Já na letra (b) para testarmos os algoritmos para solucionarmos tendo
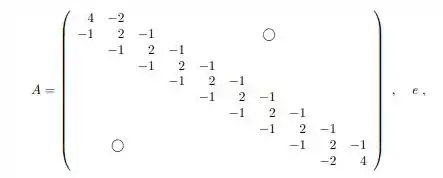
Com,
Temos,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta
a)
b)