- Esboce os gráficos de e .
- Use o método da bisseção para encontrar uma aproximação dentro de para o primeiro valor positivo de com .
Passo 1
Falaiii meus amores, cêis tão suave?
Bora pra mais uma??
Então, encostaa!!
- Deixe
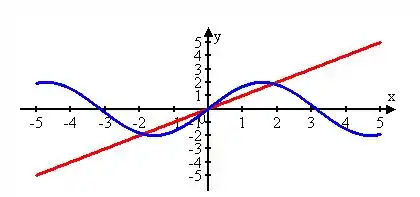
- Partindo do gráfico
Os gráficos são mostrados logo abaixo, de ,
Passo 2
Temos
Portanto, a raiz está em [1.8, 1.9]
Onde,
Portanto, a raiz está entre
Agora,
Onde
Portanto, a raiz está entre
Agora,
Onde
Portanto, a raiz está entre
Passo 2
Agora,
Onde
Portanto, a raiz está entre
Agora,
Onde
Portanto, a raiz está entre
Agora,
Onde
Portanto, a raiz está entre
Passo 3
Agora,
Onde
Portanto, a raiz está entre
Agora,
Onde
Portanto, a raiz está entre
Agora,
Onde
Portanto, a raiz está entre
Passo 4
Agora,
Onde
Portanto, a raiz está entre
Agora,
Onde
Portanto, a raiz está entre
Agora,
Onde
Portanto, a raiz está entre .
Passo 5
Agora,
Onde
Portanto, a raiz está entre
Agora,
Onde
Aqui a precisão está dentro de .
Portanto, dá solução aproximada.
Resposta
Portanto, dá solução aproximada.