O método de Steffensen é aplicado a uma função usando para obter . O que é ?
Passo 1
Falaiii meus amores, cêis tão suave?
Bora pra mais uma??
Então, encostaa!!
A teoria relevante necessária para resolver o problema dado é fornecida abaixo.
Para acelerar a taxa de convergência de uma sequência linearmente convergente, independentemente de sua origem ou aplicação, é aplicada uma técnica especial chamada método de Aitken.
Passo 2
Método de Aitken: Se é uma sequência linearmente convergente com
é uma nova sequencia que converge mais rapidamente para do que a sequencia , então
Para um valor suficientemente grande d
Resolvendo a equação aproximada para p como mostrada abaixo
Passo 3
Continuando
O método de Aitken é baseado na suposição de que a sequencia definida por
Converge mais rapidamente para sequencia do que o original
Usando a notação de diferença direta
Onde
Passo 4
Método de Steffensen: É uma modificação do método de Aitken para um método linearmente convergente, a sequencia obtida da iteração de ponto fixo. Uma sequencia linearmente convergente pode ser acelerado para convergência quadrática por esta técnica. O método de Aitken , e mostrado abaixo, sua construção de termos.
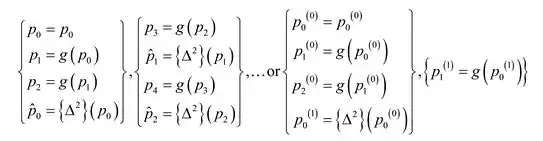
Cada terceiro termo da sequência de Steffensen é gerado
E os outros termos usa, iteração de ponto fixo no termo anterior. Se então a sequencia é encerrada e é selecionada como a melhor aproximação .
Dado que o método de Steffensen é aplicado a uma função usando e ,
Determine o valor de
Passo 5
Continuando
Passo 6
Resposta
Portanto,