Mostre que f'(x) é 0 pelo menos uma vez nos intervalos dados.
a.
b.
c.
d.
Passo 1
Fala, pessoal! Prontos para mais um exercício?
Vamos usar o Teorema de Rolle! Para quem não lembra, esse teorema afirma que existe um valor no intervalo tal que se a função satisfaz as seguintes condições:
é contínua no intervalo
é derivável no intervalo
Passo 2
Vamos então verificar se as três condições são satisfeitas para as funções dadas, começando pela letra (a).
Na figura abaixo, vemos o gráfico de . Em uma análise visual, é possível verificar que a função é contínua no intervalo dado. De fato, sua lei de formação está definida para todos os pontos do intervalo e não apresenta nenhum salto.
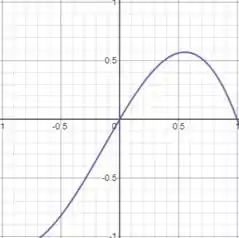
Calculando a derivada de , obtemos .
Na figura abaixo, vemos o gráfico de . Em uma análise visual, é possível verificar que a função também é derivável no intervalo dado. De fato, sua lei de formação está definida para todos os pontos do intervalos e não apresenta nenhum salto.
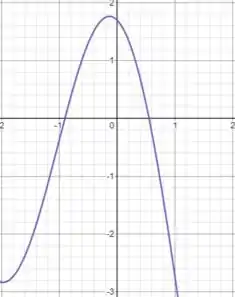
Por fim, temos que , isto é, a terceira condição é satisfeita.
Logo, podemos afirmar que é 0 pelo menos uma vez no intervalo .
Passo 3
Na letra (b), temos e . Logo, podemos afirmar que pelo menos uma vez no intervalo .
Na letra (c), temos e . Logo, no intervalo , podemos afirmar que pelo menos uma vez.
Na letra (d), temos e e . Como são valores distintos, precisamos achar um subintervalo que satisfaz o teorema. Note que . Logo, no intervalo , podemos afirmar que é nula pelo menos uma vez.
Observe que, para todos os casos, a lei de formação da função e de sua derivada estão bem definidas para todos os pontos do intervalo de interesse, sem apresentar saltos, e por isso consideramos que as condições 1 e 2 foram satisfeitas.
Resposta
No desenvolvimento.