Repita o Exercício 13, assumindo que a terceira derivada de f é limitada em [1, 5] por 4.
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
Vamos considerar os seguintes dados
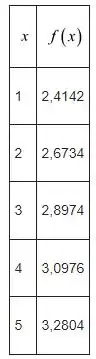
Passo 2
Para aproximar usando , a fórmula do ponto médio de cinco pontos
Tomando
Logo,
Passo 3
O erro na fórmula do ponto Médio de cinco pontos dados por
Também é dado que a 3ª derivada de ou seja é limitada por 4 em [1,5].
Portanto, o erro limitado na aproximação
Resposta
Portanto, o erro limitado na aproximação