Representemos por o número das unidades de n produtos que podem ser produzidos no decorrer de uma semana. Para produção de cada unidade precisa-se de m tipos diferentes de matéria prima . Tais relações são dadas através de uma matriz onde indica quantas unidades da matéria prima são necessárias para produzir uma unidade do produto . Suponha que existam unidades respectivamente de matérias primas . Nosso problema é determinar quantas unidades de cada produto podemos produzir. Lembre-se que tais quantidades devem ser inteiras e não negativas. Considere os dados da Tabela abaixo.
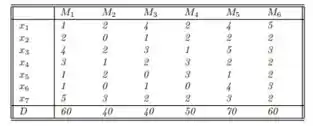
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de cálculo numérico de Franco e Neide se representarmos por o número das unidades de n produtos que podem ser produzidos no decorrer de uma semana. Para produção de cada unidade precisa-se de m tipos diferentes de matéria prima . Tais relações são dadas através de uma matriz onde indica quantas unidades da matéria prima são necessárias para produzir uma unidade do produto . Suponha que existam unidades respectivamente de matérias primas . Nosso problema é determinar quantas unidades de cada produto podemos produzir. Lembre-se que tais quantidades devem ser inteiras e não negativas. Considere os dados da Tabela abaixo.
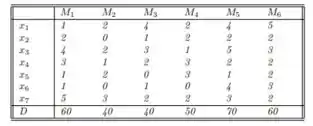

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galerinha nessa questão ele deseja saber a quantidade de unidades inteiras e não negativas que devem usar sabendo que na tabela dada acima os somatórios de são,
Logo temos que,
Ficando,
Sendo os valores inteiros e não negativos.
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta
São valores inteiros e não negativos.