Seja e . Use o método de Steffensen para encontrar .
Passo 1
Falaiii meus amores, cêis tão suave?
Bora pra mais uma??
Então, encostaa!!
A teoria relevante necessária para resolver o problema dado é informado abaixo.
Para acelerar a taxa de convergência de uma sequência linearmente convergente, independentemente de sua origem ou aplicação, é aplicada uma técnica especial chamada método de Aitken .
Passo 2
Método de Steffensen: É uma modificação do método de Aitken para um método linearmente convergente sequencia obtida da iteração de ponto fixo. Uma sequencia linearmente convergente pode ser acelerado para convergência quadrática por esta técnica.
O método de Aitken constrói os termos na ordem mostrada abaixo.
Cada terceiro termo da sequência de Steffensen é gerado para e os outros termos usam iterações de ponto fixo no termo anterior. Se então a sequência é encerrada e é selecionada como a melhor aproximação.
Considere a função e
Usando o método de Steffensen para encontrar usando a tecnologia Maple, conforme mostrado a seguir:
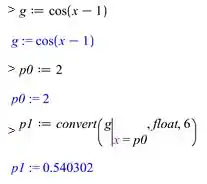
Passo 3
Continuando
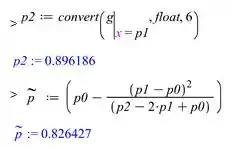
Resposta
Logo, a aproximação necessária é