uma. Suponha que 0
b. Faça uma tabela listando 1/n, 1/n2, 1/n3 e 1/n4 para n = 5, 10, 100 e 1000 e discuta o
variando as taxas de convergência dessas sequências à medida que n se torna grande.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Taxa de convergência: Suponha, é uma sequência converge para zero e é outra sequência que converge para um número real . Se existe um número real positivo , como então, diz-se que a sequência converge para um número real com taxa, ou ordem, de convergência.
Matematicamente é denotado por .
Em geral é representado como para algum número real e . Se o valor de é muito grande, então a taxa de convergência da sequência é mais rápida.
Passo 2
a) Para provar que
Dado que e , consideramos que
Considerando que isso implica que a sequência é dito para convergir para um número real com taxa, ou ordem, de convergência
Assim, provamos 😊
Passo 3
b) Tabular a listagem , e , para e como mostrado abaixo.
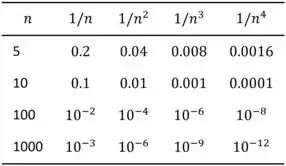
Da tabela acima, ele infere que converge a uma velocidade mais rápida.
Resposta
Resposta nos passos.