Suponha que uma membrana com dimensões tenha cada um dos seus lados mantidos a uma temperatura constante. Usando a teoria de equações diferenciais parciais pode-se formular uma equação que determina o valor da temperatura no interior dessa membrana. Essa equação diferencial pode ser simplificada colocando-se uma malha com 9 pontos sobre essa membrana e calculando-se a temperatura nos pontos da malha, como mostra a figura:
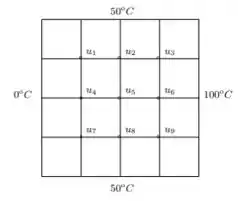
onde são os valores da temperatura em cada ponto da malha. O sistema de equações resultante ´e dado por:
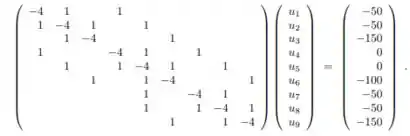
Encontre a solução do sistema por método numérico à sua escolha, com garantia de convergência.
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de cálculo numérico de Franco e Neide supondo que uma membrana com dimensões tenha cada um dos seus lados mantidos a uma temperatura constante. Usando a teoria de equações diferenciais parciais pode-se formular uma equação que determina o valor da temperatura no interior dessa membrana. Essa equação diferencial pode ser simplificada colocando-se uma malha com 9 pontos sobre essa membrana e calculando-se a temperatura nos pontos da malha, como mostra a figura:
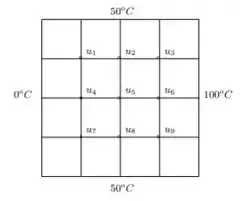
onde são os valores da temperatura em cada ponto da malha. O sistema de equações resultante ´e dado por:
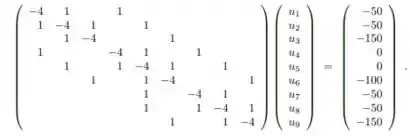
Encontre a solução do sistema por método numérico à sua escolha, com garantia de convergência.

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galera nessa questão ele pede para determinarmos a solução do sistema por método numérico sendo com base nas imagens do passo anterior que,
Ficando,
Com isso temos que,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta