Suponha que tenhamos um circuito que consiste de fontes de tensão independentes e resistores concentrados como mostra a figura:
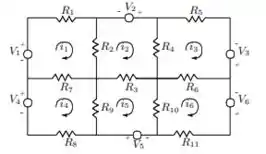
A análise completa de tal circuito requer a determinação dos valores das correntes da malha , indicados na figura, para os valores especificados das fontes de tensão e dos resistores. é necessário, então, formular um sistema de equações simultâneas com as quantidades como incógnitas. Cada uma das equações de tal sistema é determinada pela aplicação da lei de Kirchoff em torno das malhas. Por exemplo, para a malha definida pela corrente , temos:
Fazendo um cálculo semelhante para as outras malhas obtemos um sistema de 6 equações nas incógnitas .
Resolver este problema para os seguintes dados:
e
Onde em ohms e em volts.
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de cálculo numérico de Franco e Neide supondo que tenhamos um circuito que consiste de fontes de tensão independentes e resistores concentrados como mostra a figura:
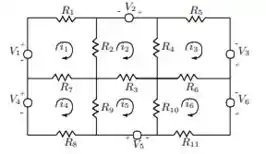
A análise completa de tal circuito requer a determinação dos valores das correntes da malha , indicados na figura, para os valores especificados das fontes de tensão e dos resistores. é necessário, então, formular um sistema de equações simultâneas com as quantidades como incógnitas. Cada uma das equações de tal sistema é determinada pela aplicação da lei de Kirchoff em torno das malhas. Por exemplo, para a malha definida pela corrente , temos:
Fazendo um cálculo semelhante para as outras malhas obtemos um sistema de 6 equações nas incógnitas .
Resolver este problema para os seguintes dados:
e
Onde em ohms e em volts.

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galera nessa questão ele pede para resolver o sistema das malhas dado:
Tendo sido fornecido,
E para temos,
Ficando,
Logo temos o conjunto de .
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta