- Use o Algoritmo 3.2 para construir o polinômio interpolador de grau três para o
pontos espaçados dados na tabela a seguir:
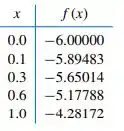
- Adicione à tabela e construa o polinômio interpolador de grau quatro.
pontos espaçados dados na tabela a seguir:

Passo 1
Boraaa galerinha, aniimaaa, vamos resolver mais um!!
Só bora então!!
- O objetivo é construir um polinômio interpolador de grau quarto.
- Adicione como sexto nó à tabela e atribua valores adicionais de diferenças divididas conforme mostrado na tabela 4.
Iremos escrever a fórmula da diferença dividida de Newton para o polinômio interpolador de quarto grau
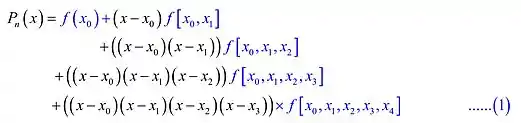
Passo 2
Vamos construir a tabela de diferenças divididas de Newton correspondente a x e f(x) conforme mostrado na tabela 1

Vamos considerar os pontos desigualmente espaçados nos valores fornecidos de x e f(x) mostrado na tabela 2
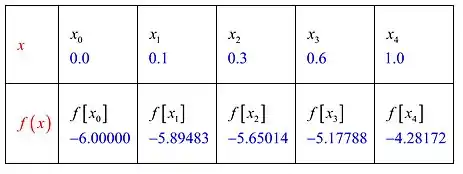
Tabela 2
Passo 3
Vamos calcular a primeira diferenças divididas:
Calculando com os dados disponíveis na Tabela 2, temos
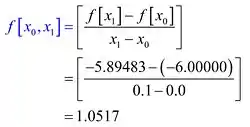
Calculando
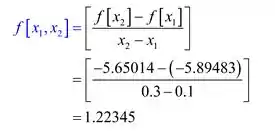

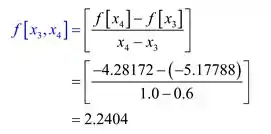
Calculando a segunda diferença dividida, temos
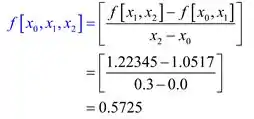
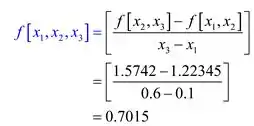
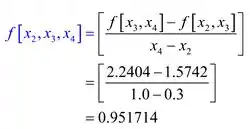
Calculando a terceiras diferenças divididas
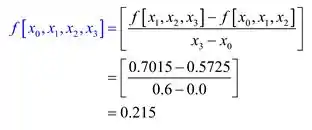
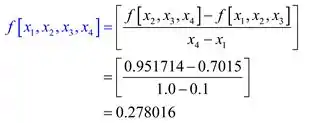
Calculando as quartas diferenças divididas:
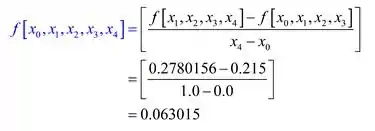
Passo 4
Substituindo todas as ordens de valores de diferença divididos na tabela 1, conforme mostrado na tabela 3.
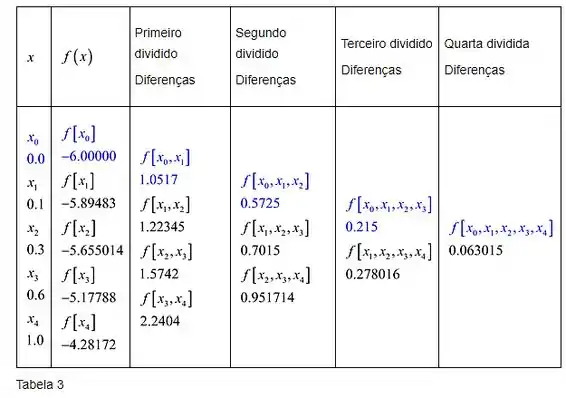
Substituindo todos os valores de diferença divididos da tabela 3 na expressão (1) para podermos obter o polinômio de interpolação de quarto grau, teremos

Passo 5
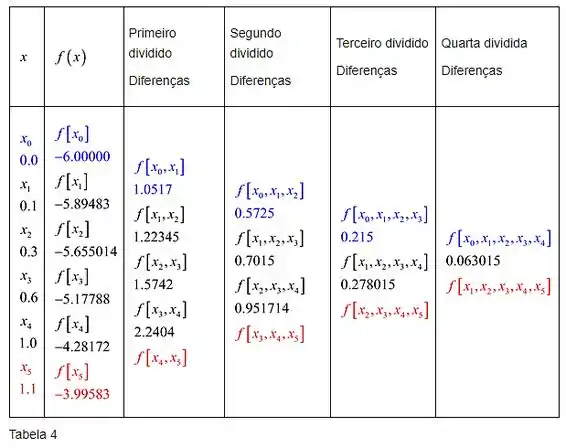



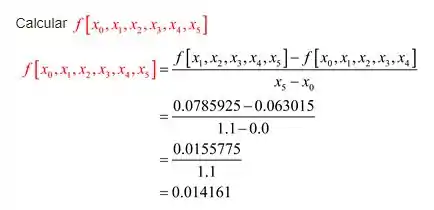
Iremos substituir todas as diferenças dividis]das na Tabela 4 conforme mostra a tabela a seguir.
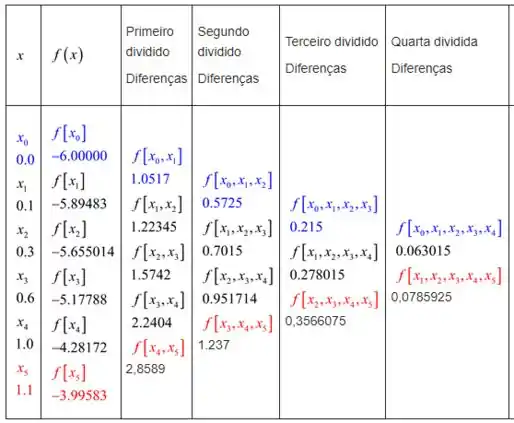
Passo 2
Vamos substituir todos os valores de diferença divididos da tabela 5 na equação (1) para podermos obter o polinômio de interpolação de quinto grau

Resposta
Vide o passo a passo.