Use o método da bisseção para encontrar soluções com precisão de para em cada intervalo.
- [0,1] b. [1,3,2]c. [3,2,4]
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
- Vamos começar, por método de bisseção:
- Deixaremos como . Como existe uma mudança de sinal, aplicando o resultado do teorema do valor intermediário acima, a função é contínua, então existe tal que .
- Deixaremos como . Como existe uma mudança de sinal, aplicando o resultado do teorema do valor intermediário acima, a função é contínua, então existe tal que .
Se . O método da bisseção gera uma sequência que se aproxima de zero de f com .
Por definição do teorema do valor intermediário,
Se é qualquer número entre então existe um número c em para o qual .
Deixaremos como . Como existe uma mudança de sinal, aplicando o resultado do teorema do valor intermediário acima, a função é contínua, então existe tal que
Deixaremos com .
Suponha que
Passo 2
Assim, como
Então
Portanto,
Podemos observar que e são de mesmos sinal, logo,
Portanto,
Logo,
Então
Portanto,
Passo 3
Os valores encontrados acima são tabulados conforme mostrado abaixo. As duas primeiras entradas são encontradas conforme mostrado acima, continuando da mesma forma, o resultado obtido é tabulado conforme mostrado na tabela a seguir:
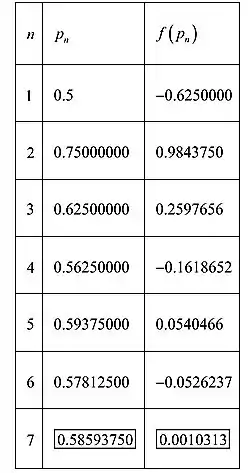
Podemos observar pela tabela que os valores continuam diminuindo até seis e as sete começam a aumentar novamente. Logo, as soluções precisas no local são para a interação com .
Passo 4
Deixaremos
Portanto
Portanto,
Similarmente,
Quando:
Seguindo o método como mostramos na etapa (a), os valores encontrados acima são tabulados conforme mostrado abaixo. As duas primeiras entradas são encontradas conforme mostrado acima, continuando da mesma forma, o resultado obtido é tabulado conforme mostrado na tabela a seguir:
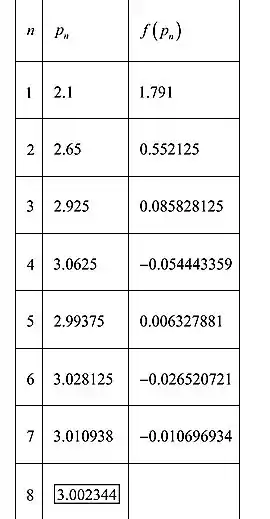
Sendo assim, as soluções precisas no local são para a interação com .
Passo 5
Deixaremos .
Portanto
Portanto,
Seguindo o método como mostramos na etapa (a), os valores encontrados acima são tabulados conforme mostrado abaixo. As duas primeiras entradas são encontradas conforme mostrado acima, continuando da mesma forma, o resultado obtido é tabulado conforme mostrado na tabela a seguir:
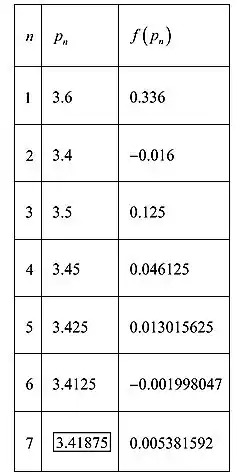
Sendo assim, as soluções precisas no local são para a interação com .
Resposta
- Logo, as soluções precisas no local são para a interação com .
- Sendo assim, as soluções precisas no local são para a interação com .
- Sendo assim, as soluções precisas no local são para a interação com .