Use o método de Euler modificado para aproximar as soluções para cada um dos seguintes valores iniciais problemas e comparar os resultados com os valores reais
.
.
Passo 1
Falaiii meus xuxu’s, ceis tão bonzinho??
Espero que sim hein, bora lá pra mais uma?
Encostaaaa
a) Para o problema de valor inicial, temos
A solução exata dada é
Comparando a equação diferencial dada com a forma geral do problema inicia
Para obter
Onde
O método de Euler modificado de ordem dois é
Agora
Logo
A tabela mostrada a seguir fornece a comparação entre a solução aproximada e a solução exata
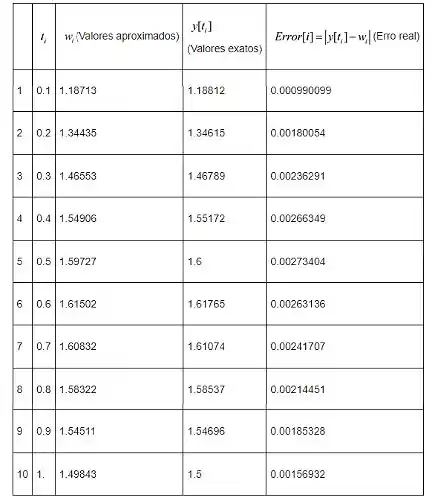
Passo 2
b) Para o problema de valor inicial, temos
A solução exata dada é
Comparando a equação diferencial dada com a forma geral do problema inicia
Para obter
Onde
O método de Euler modificado de ordem dois é
Agora
Logo
A tabela mostrada a seguir fornece a comparação entre a solução aproximada e a solução exata
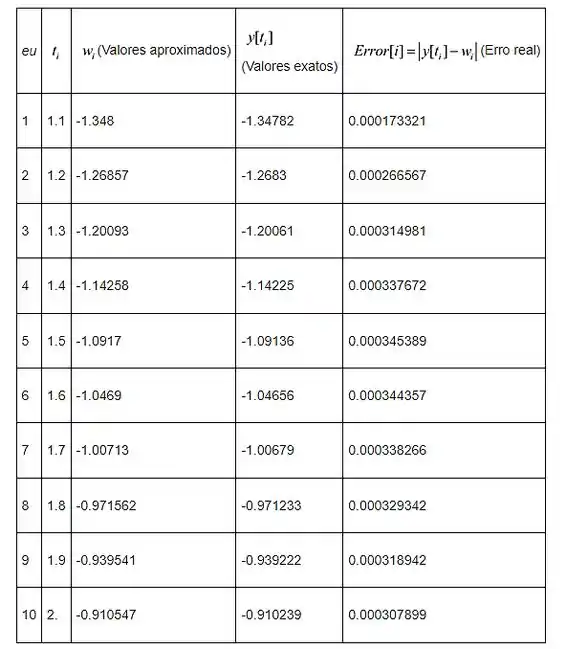
Passo 3
c) Para o problema de valor inicial, temos
A solução exata dada é
.
Comparando a equação diferencial dada com a forma geral do problema inicia
Para obter
Onde
O método de Euler modificado de ordem dois é
Agora
Logo
A tabela mostrada a seguir fornece a comparação entre a solução aproximada e a solução exata
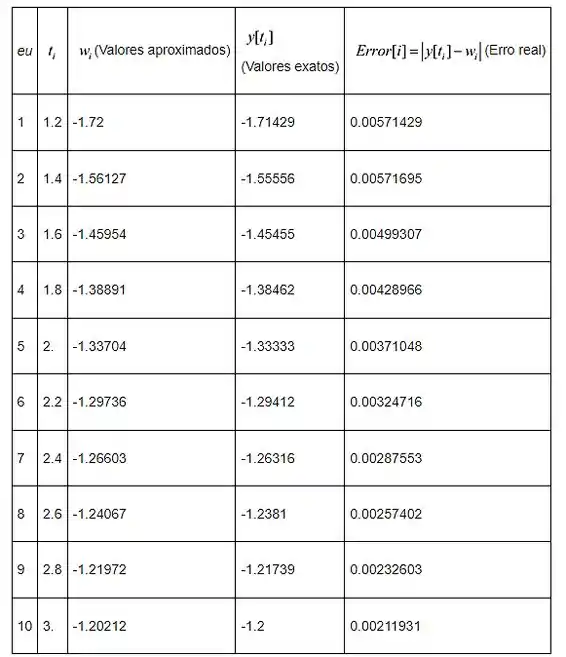
Passo 4
d) Para o problema de valor inicial, temos
A solução exata dada é
Comparando a equação diferencial dada com a forma geral do problema inicia
Para obter
Onde
O método de Euler modificado de ordem dois é
Agora
Logo
A tabela mostrada a seguir fornece a comparação entre a solução aproximada e a solução exata
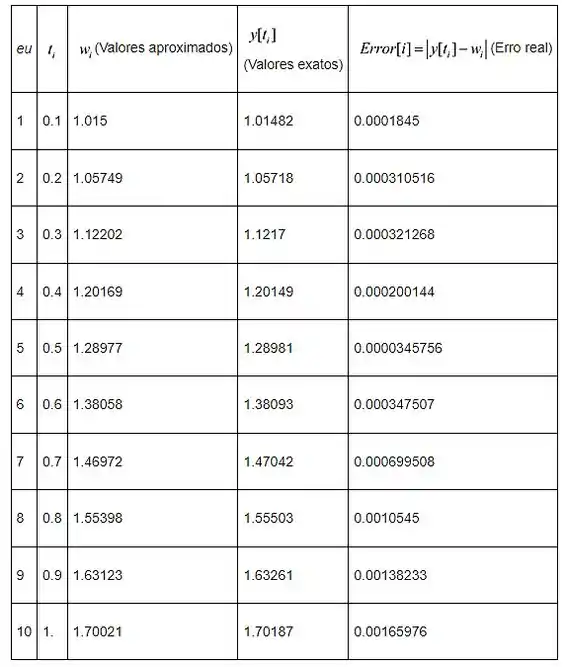
Resposta
Vide a explicação.