Use o método de Newton para encontrar soluções com precisão de 10^−5 para os seguintes problemas.
d.
e.
f.
Passo 1
Falaa galerinhaa!!! Tudo certinhoo?? Bora juntos pra mais uma!
Nessa questão, precisamos relembrar o método de Newton, dado por:
Certo, nós vamos usar essa fórmula pra todos os itens dessa questão, ok?
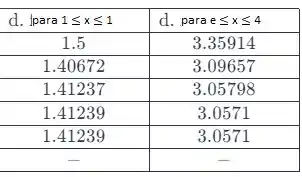
Pra aplicarmos ela, vamos encontrar a derivada da função dada. Começando pela letra d, temos a seguinte tabelinha:
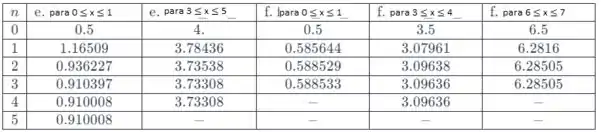
Na letra e e f, temos:
Certo, assim, conseguimos encontrar pelas iterações, que:
Para a letra d, temos entre 1 e 2: 1.41239.
Para a letra d, temos entre e e 4: 3.0571.
Para a letra e, temos entre 0 e 1: 0.910008.
Para a letra e, temos entre 3 e 5: 3.73308.
Para a letra f, temos entre 0 e 1: 0.588533.
Para a letra f, temos entre 3 e 4: 3.09636
Para a letra f, temos entre 6 e 7: 6.28505.
Prontinho, galera!! Bora juntos pra próxima
Resposta
d. Entre 1 e 2: 1.41239. Entre e e 4: 3.0571.
e. Entre 0 e 1: 0.910008. Entre 3 e 5: 3.73308.
f. Entre 0 e 1: 0.588533. Entre 3 e 4: 3.09636. Entre 6 e 7: 6.28505.