Use os seguintes dados e saiba que as cinco primeiras derivadas de f são limitadas em [1, 5] por 2, 3, 6, 12 e 23, respectivamente, para aproximar f (3) com a maior precisão possível. Encontre um limite para o erro.
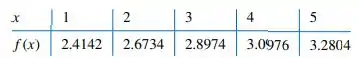
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
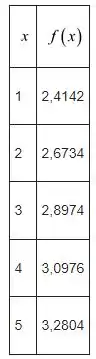
Vamos considerar os seguintes dados
Passo 2
Para aproximar usando , a fórmula do ponto médio de cinco pontos
Tomando
Logo,
Passo 3
O erro na fórmula do ponto Médio de cinco pontos dados por
Também é dado que a 5ª derivada de ou seja é limitada por 23 em [1,5].
Portanto, o erro limitado na aproximação
Resposta
Portanto, o erro limitado na aproximação