Crescimento, Decrescimento, Máximos e Mínimos
Teoria
Quem nunca precisou do gráfico de uma função, mas olhando pra expressão não tinha nem ideia de por onde começar?
Bom, eu já passei por isso várias vezes, mas vim avisar que não precisa ser sempre assim!
Hoje eu to aqui pra te ensinar como usar derivadas para entender um pouco do comportamento de uma função. Vamos focar em dois aspectos principais: identificar as regiões onde uma função cresce ou decresce, e identificar os pontos de máximo e mínimo de uma função.
Com isso já dá pra ter uma ideia legal de como é o gráfico da função!
Identificar as regiões de Crescimento e Decrescimento de uma função:
Pra começar, precisamos lembrar que a derivada de uma função é também a inclinação da reta tangente ao gráfico da função em cada ponto, já que isso mostra muito sobre o crescimento ou decrescimento das funções. Observe o gráfico:
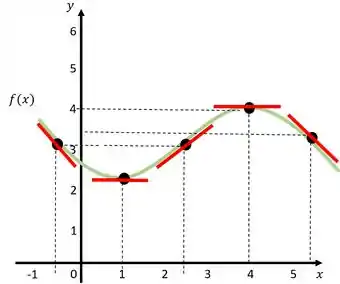
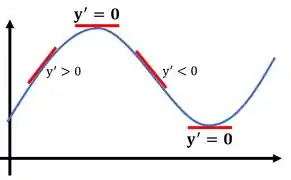
Em verde, temos o gráfico de uma função qualquer, e em vermelho, as retas tangentes à função correspondentes a cada ponto. Perceba que a função começa decrescendo, até que chega no ponto mais baixo em , depois ela começa a crescer até chegar no ponto mais alto em , então ela volta a decrescer novamente.
Perceba também que as retas tangentes tem uma inclinação negativa (como se estivesse apontando pra baixo) quando a função é decrescente, e positiva (apontando pra cima) quando a função é crescente .Já no ponto mais baixo e no ponto mais alto elas não possuem inclinação, estão na horizontal. E com essa informação nós podemos encontrar os intervalos onde a função é crescente e onde a função é decrescente:
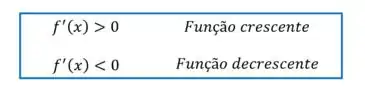
Sendo assim, só precisamos derivar a função e ver em qual intervalo essa derivada é maior ou menor que zero.
Vamos ver um exemplo:
Determine em que intervalos a função é crescente e decrescente.
Passo 1: Calcular a derivada da função
Passo 2: Avaliar a condição para que a função seja crescente
Resolvendo a inequação, temos:
Assim, vemos que a função é crescente para valores de maiores que . Podemos dizer também que ela é crescente no intervalo .
Passo 3: Avaliar a condição para que a função seja decrescente
Resolvendo a inequação, temos:
Assim, vemos que a função é decrescente para valores de menores que . Podemos dizer também que ela é decrescente no intervalo .
Beleza, mas e os pontos onde a reta tangente não possuía inclinação?
Determinar pontos de Máximos e Mínimos de uma função:
Vimos que nossa derivada vai ser negativa quando a inclinação da reta tangente for para baixo, e positiva quando a inclinação da reta tangente for para cima, mas olhando novamente para o gráfico podemos identificar alguns pontos onde as retas tangentes são horizontais e tem inclinação igual a zero. Vamos chamar os pontos onde isso acontecer de pontos críticos.
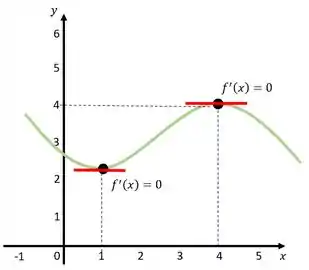
Agora repara como o primeiro ponto crítico é o ponto de mínimo da função e o segundo é o ponto de máximo. Isso não é coincidência! Os máximos e mínimos de uma função sempre acontecem em pontos críticos.
Então, se quisermos encontrar os pontos de máximo e mínimo de uma função, precisamos achar os pontos críticos, igualando a derivada da função a zero, e depois testar os valores encontrados para descobrir se são pontos de máximo ou mínimo.
Pra fazer esse teste, precisamos calcular a segunda derivada da função e então considerar os critérios:
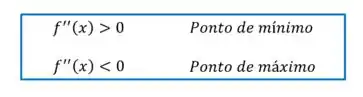
Obs.: Quando a derivada segunda for igual a zero, temos um ponto de inflexão, mas pro assunto de hoje eles não são importantes, então não precisa esquentar a cabeça.
Vamos a um exemplo pra tudo ficar mais claro:
Determine os pontos de máximo e mínimo da função .
Passo 1: Calcular a derivada da função
Passo 2: Encontrar os pontos críticos fazendo
Aqui, temos uma equação do 2º grau, então precisamos usar a fórmula de Bháskara para encontrar a solução:
Esses são nossos candidatos a máximo e mínimo. Bora pro teste da segunda derivada!
Passo 3: Calcular a segunda derivada da função
Pra isso, pegamos a derivada que calculamos no passo 1 e derivamos mais uma vez:
Passo 4: Fazer o teste da derivada segunda pra saber se os pontos críticos são máximos ou mínimos da função
O teste da derivada segunda diz que:
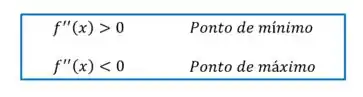
Então, vamos fazer o teste para cada ponto, começando pelo ponto
Substituindo o ponto na segunda derivada, temos:
Como a segunda derivada foi maior que zero, nosso ponto é um ponto de mínimo.
Agora vamos testar o ponto , substituindo:
Como a derivada segunda é negativa, temos um ponto de máximo.
Podemos ver isso, também graficamente:
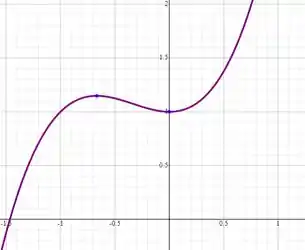
OBS: Repara que apesar de chamarmos de máximo e mínimo, os dois pontos não são necessariamente o maior ou menor valor da função.
Nesse caso, o é um ponto de máximo local, o que significa que naquela região a função formou uma “montanha” e ele é o topo.
De forma parecida, o é um ponto de mínimo local, já que é o menor ponto do vale formado pela função naquela região.
Apesar de não ter acontecido aqui, os pontos críticos da função também podem indicar o maior ou o menor valor da função inteira, quando isso acontece, chamamos de ponto de máximo ou de mínimo global.
Agora que já vimos bastante coisa, bora para os exercícios praticar!!!
Determinar pontos de Máximos e Mínimos de uma função:
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Determine os intervalos onde a função abaixo cresce e decresce:
Passo 1
Fala aí!
A questão pede para encontrarmos os intervalos onde a função cresce e decresce, pra isso precisamos calcular sua derivada.
Isso porque a derivada representa a inclinação da reta tangente a função. Quando o gráfico de uma função está descendo a reta tangente a ele estará inclinada negativamente, e quando estiver subindo, sua tangente estará inclinada para cima.
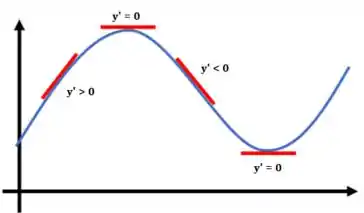
Então, nos intervalos onde a derivada da função for positiva , a função está crescendo e quando for negativa , está decrescendo.
Passo 2
Para começar, precisamos derivar a função:
Vamos usar a regra do peteleco
E lembrando que derivada de constante é zero, temos:
Passo 3
Agora, vamos montar a primeira inequação para encontrar o intervalo onde a derivada é positiva, ou seja, maior que zero:
Para tirarmos o sinal de negativo do , vamos multiplicar toda a inequação por , quando fazemos isso invertemos também o sinal de maior para menor:
Então, quando é menor que , a derivada é positiva e a função está crescendo!
Passo 4
Agora fazemos o mesmo processo, mas para encontrar o intervalo onde a derivada é negativa:
De novo, multiplicamos toda a expressão por :
Quando é maior que , a derivada é negativa e a função está decrescendo!
Se quisermos conferir se os intervalos que encontramos estão certinhos, podemos conferir o gráfico da função:
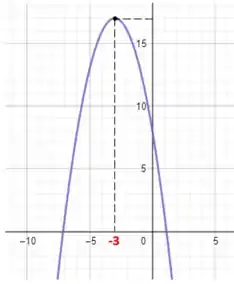
Como podemos ver, a função cresce antes de e depois decresce!
Resposta
A função cresce quando e decresce quando .
Exercício Resolvido #2
Seja . Determine o(s) intervalos onde a função é decrescente
(a)
(b) Nenhuma das respostas
(c)
(d)
(e)
Passo 1
Opa! Tudo joia?
Olha só: uma função é decrescente nos pontos em que a sua derivada é negativa. Veja o exemplo desse gráfico aqui:
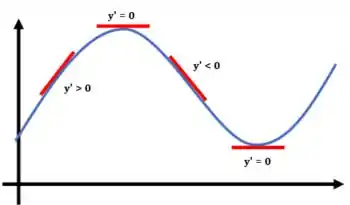
Vamos achar a derivada de então!
A gente vai usar a regra do tombo, beleza?
Essa aqui:
Passo 2
Aplicando essa regra na nossa função, fica assim:
(Lembra que derivada de constante é zero e que 😊)
Passo 3
A gente quer os pontos onde a derivada é negativa, ou seja:
Vamos resolver essa inequação, então!
Pra tirar esse quadrado do , podemos colocar raiz quadrada dos dois lados da equação:
Mas quando fazemos isso, precisamos colocar um módulo no :
Passo 4
Pra finalizar, vamos lembrar que o módulo pode ter dois resultados, positivo ou negativo:
Como nessa segunda temos um , pra deixá-lo positivo, nós multiplicamos tudo por , o que no final das contas, vai mudar o sinal de todo mundo, incluindo o sinal de que vai virar :
Com isso, temos que:
- ( é maior que )
- ( é menor que
Com isso, o intervalo onde a derivada é negativa é entre e , que escrevendo em matematiquês fica:
E esse é o intervalo onde a função é decrescente! 😊
Resposta
Exercício Resolvido #3
Elaboração Própria
Determine os intervalos onde a função abaixo cresce e decresce:
Passo 1
E aí, tudo bom?
Queremos encontrar os intervalos onde a função cresce e decresce e vamos fazer isso usando derivadas!
Pra isso, precisamos lembrar que a derivada representa a inclinação da reta tangente à função. Quando o gráfico de uma função está descendo, a reta tangente a ele estará inclinada pra baixo, e quando estiver subindo, sua tangente estará inclinada para cima.
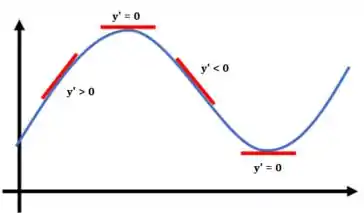
Então, nos intervalos onde a derivada da função for positiva , a função está crescendo e quando for negativa , está decrescendo.
Passo 2
Para começar, precisamos derivar a função:
Vamos usar a regra do peteleco
E lembrando que derivada de constante é zero, temos:
Passo 3
Precisamos descobrir os intervalos onde essa função é positiva e negativa, como temos uma função do 2º grau, vamos fazer um esboço do gráfico.
Primeiro, vamos descobrir as raízes, ou seja, os pontos onde a função é igual a zero:
Pra facilitar nossas contas, vamos dividir toda a expressão por :
Agora, vamos resolver usando a fórmula de Bhaskara:
Identificando os termos da nossa equação:
Substituindo na primeira fórmula:
Seguindo pra segunda:
Assim sendo, temos:
Então, as raízes da equação são e .
Passo 4
Para esboçar o gráfico, precisamos saber se a concavidade é pra cima ou pra baixo. Isso é definido pelo coeficiente da função do 2º grau: quando , temos concavidade para cima, e quando , temos concavidade para baixo.
Olhando para a derivada:
Temos , então a concavidade é para cima.
Passo 5
Finalmente, podemos fazer o esboço do gráfico, traçando uma parábola que passa pelos pontos e no eixo e que tenha concavidade para cima.
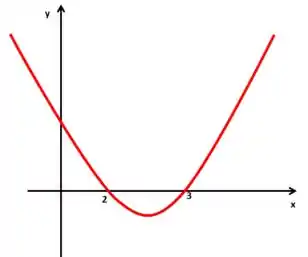
Olhando pro nosso esboço podemos ver que a derivada só é negativa no intervalo entre e , tanto pra , quanto pra , a derivada é positiva.
Como a função decresce quando a derivada é negativa, temos a função decrescendo para entre e .
E como a função cresce quando a derivada é positiva, temos a função crescendo para ou para .
Intervalos encontrados! Prontinho!
Resposta
A função cresce quando ou , e decresce quando .
Exercício Resolvido #4
Determine o ponto crítico da função
- 3 e 4
- Nenhuma das respostas anteriores
- 2 e 3
- 3
- 0
Passo 1
Fala aí, tudo beleza? Essa aqui é outra aplicação das derivadas!
Vamos encontrar um ponto crítico da função, que é um ponto bem especial.
A derivada representa a inclinação da reta tangente ao gráfico em determinado ponto. Chamamos de ponto crítico, um ponto que pode ser de máximo, ou de mínimo da nossa função. Nesses pontos a reta tangente fica na horizontal e não tem inclinação, com isso a derivada será igual a zero.
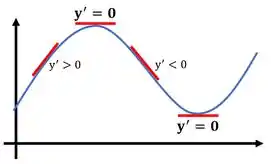
Por hora, vamos aprender a calcular esse ponto...
Então para determinarmos o ponto crítico, vamos encontrar a primeira derivada da nossa função e depois igualar ela a zero, vamos lá?
Passo 2
Nossa função é:
A gente deriva com a regra do Tombo, que a gente já aprendeu lá atrás, descendo o expoente pra frente e perdendo 1 no novo expoente. Vai ficar assim:
Como todo número elevado a zero é 1...
Essa é a nossa derivada!
Passo 3
Agora vamos igualar a derivada que achamos a zero ...
Prontinho! Esse é o nosso ponto crítico da função. Quer dizer que ele pode ser um ponto de valor máximo ou de valor mínimo! Como não sabemos qual dos dois, chamamos apenas de ponto crítico. 😉
Resposta
d) 3.
Exercício Resolvido #5
Determine qual(is) são os pontos críticos da função .
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala aí, tudo joia?
Olha só, ponto crítico é onde a derivada é zero, beleza?
Isso porque a derivada é a inclinação da reta tangente ao gráfico. Um ponto crítico é um ponto onde a função atinge seu valor máximo ou mínimo, nesses pontos a reta tangente fica completamente na horizontal. Sendo assim, ela não terá nenhuma inclinação, e por isso a derivada será igual a zero.
Vamos começar calculando a derivada então...
Passo 2
Vamos derivar essa função aqui:
A gente tem um polinômio, então vamos derivar usando a regra do Tombo, lembra dela?
Vamos aplicar isso na nossa função!
Passo 3
Aplicando a regra do Tombo na função , temos:
A gente ainda pode colocar o em evidência:
Passo 4
Agora que já achamos a derivada, vamos ver em que ponto ela é igual a zero, fazendo:
Pra um produto dar zero, um dos fatores tem que ser zero, como aqui temos o multiplicando o , podemos ter essas duas condições:
Resolvendo essa segunda equação...
Passo 5
Beleza! Achamos os dois pontos críticos então, que são:
E é só isso por aqui😊
Resposta
(d)
Exercício Resolvido #6
Determine os pontos da função , nos quais as retas tangentes são horizontais.
Passo 1
Antes de tudo, precisamos lembrar que a derivada de uma função é representada pela inclinação da reta tangente ao gráfico daquela função em determinado ponto:
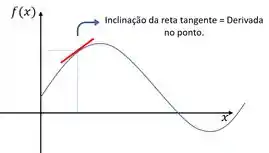
Como o enunciado tá dizendo que a reta tangente é horizontal, ela não terá inclinação e vai ficar tipo assim no gráfico:
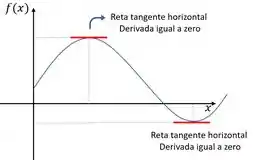
Em outras palavras, a derivada será igual a zero. E o que ele está querendo saber é qual é o ponto que faz isso acontecer. Repara que isso acontece quanto a função tem seus valores máximos e mínimos, também chamado de pontos críticos.
Então pra descobrir esses valores de , vamos precisar derivar essa nossa função e igualar a zero. Partiuuu!!!
Passo 2
Começamos pela derivada:
Lembra que temos a propriedade em relação a soma, onde podemos calcular a derivada de cada termo
Pra essa vamos fazer a regra do peteleco e não mexemos na constante, certo?
A próxima derivada vai ser no mesmo esquema da anterior, regrinha do peteleco e não mexemos na constante
O último é a derivada de uma constante, que é zero
Logo
Passo 3
Igualando a zero, teremos
Virou uma equação que podemos resolver isolando o , jogando o que está subtraindo, para o outro lado.
Agora é a vez de jogar o 3 que tá multiplicando, para o outro lado dividindo:
Temos:
Agora a pergunta é: Qual o valor que quando elevado ao quadrado dá 4?
Há duas possibilidades:
Porque ambos elevados ao quadrado resultam em
Passo 4
Agora vamos substituir esses valores na nossa função original
Primeiro para
Ou seja, o primeiro ponto é formado pelas coordenadas .
Agora vamos fazer para o
Ou seja, o segundo ponto é
Resposta
Exercício Resolvido #7
Elaboração Própria
Seja a função . Determine o valor máximo assumido por essa função.
8
Passo 1
Bom, a questão pede pra encontrarmos o valor máximo assumido pela função, então precisamos encontrar os pontos críticos e checar se são de máximo ou mínimo.
Bora lá!
Passo 2
A primeira coisa a se fazer para encontrar os pontos críticos de uma função, é calcular sua derivada:
Usando a regra do peteleco, temos:
Passo 3
Os pontos críticos estarão nos pontos onde a derivada for igual a zero, vamos então igualar a derivada que encontramos a zero e resolver a equação formada:
Então, é o ponto crítico dessa função!
Passo 4
Agora precisamos conferir se esse é um ponto de máximo ou de mínimo, pra isso, vamos calcular a segunda derivada da função:
O critério é o seguinte:
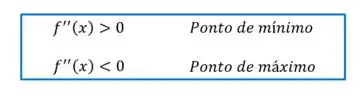
Como da nossa função é sempre negativa, o ponto crítico é um ponto de máximo, exatamente como queríamos!
Passo 5
Pra encerrar, a questão pediu o valor máximo assumido pela função, ou seja, queremos saber quanto vale a função no seu ponto máximo.
Vamos então calcular para :
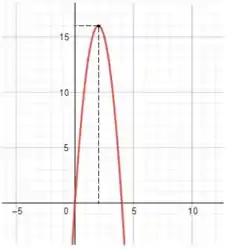
Então, o valor máximo assumido pela função quando é .
Se traçarmos o gráfico da função, conseguimos ver direitinho:
Resposta
Exercício Resolvido #8
Algumas das aplicações mais importantes do cálculo diferencial são os problemas de otimização, em que devemos encontrar a maneira ótima (melhor maneira) de fazer alguma coisa. Um bom jeito de achamos essa maneira é avaliando os pontos de máximo e mínimo da função que descreve nosso problema.
Encontre os máximos e mínimos relativos da função .
Passo 1
E aí, tudo bem?
Aqui a primeira coisa que vamos fazer, é derivar essa nossa função e depois igualar a nossa a zero para determinarmos os pontos críticos dela:
Usamos a regra do tombo aqui: :
Passo 2
Vamos igualar essa nossa a zero:
Pra resolver essa equação do segundo grau, vamos utilizar a fórmula de Bháskara:
Sendo que aqui temos: :
Passo 3
Encontramos as coordenadas de dos nossos pontos críticos.
Agora nos resta descobrir quem é mínimo e quem é máximo. Pra isso, vamos fazer o teste da derivada segunda:
Mais uma vez, vamos usar a regra do tombo:
Passo 4
O critério do teste da segunda derivada é o seguinte:
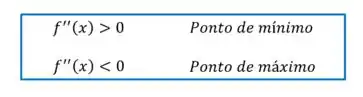
Vamos então calcular quanto vale a segunda derivada para os dois pontos críticos que encontramos:
Como a segunda derivada é positiva, é um ponto de mínimo.
Já para , como a segunda derivada é negativa, temos um ponto de máximo.
Passo 5
Pra finalizar, vamos encontrar os valores correspondentes da função para cada um dos pontos.
Para o ponto de mínimo, substituímos :
Para o ponto de máximo, substituímos :
Resposta
Exercício Resolvido #9
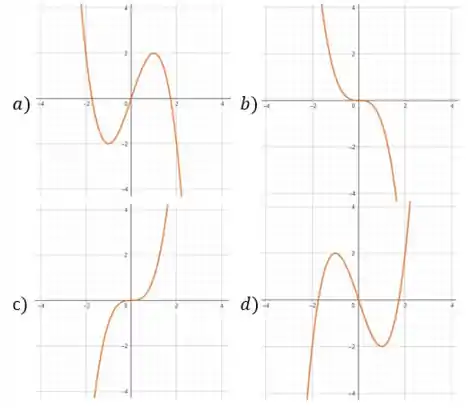
Aplicando os conceitos de derivada, qual o gráfico da função definida em por ?
Passo 1
E aí, tudo beleza?
Vamos ver qual é o gráfico dessa função aqui:
Bom, o exercício falou pra a gente usar os conceitos de derivada. A gente sabe que com a derivada podemos achar os pontos de máximo e mínimo da função, bem como os intervalos de crescimento e decrescimento. Bora lá então?
Passo 2
Bora derivar a função então! A gente vai usar a regra do tombo: .
Aplicando em :
Passo 3
Bom, os pontos críticos da função, que são nossos candidatos a ponto de máximo e mínimo são os pontos onde a derivada é zero. Vamos ver isso igualando a derivada que acabamos de encontrar a zero, então:
Beleza! Esses são os pontos críticos da função😊
Passo 4
Vamos checar então se esses pontos críticos são de máximo ou de mínimo!
Pra isso, precisarmos fazer o teste da segunda derivada, que vamos calcular usando a regra do tombo mais uma vez e lembrando que derivada de constante dá zero:
Passo 5
Pelo teste da segunda derivada, temos:
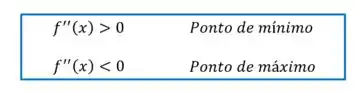
Vamos então calcular quanto vale pra cada um dos pontos críticos que encontramos:
Como é negativo quando , temos um ponto de máximo.
Como é positivo quando , temos um ponto de mínimo.
Passo 6
Agora vamos voltar aos gráficos e procurar qual deles possui um máximo em e um mínimo em .
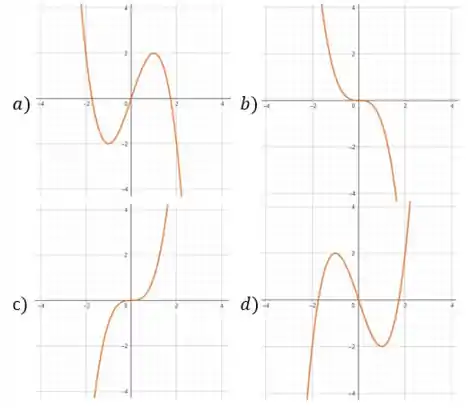
O único gráfico correspondente aos pontos que encontramos é o da alternativa , que é nossa resposta final!
Resposta
Exercício Resolvido #10
Encontre os pontos de inflexão da curva .
Passo 1
Pra ter uma ideia do que estamos falando, um ponto de inflexão é uma coisa como essa:
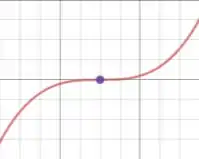
Pondemos dizer que é o ponto onde a função muda de comportamento. Repara que ela tinha uma cruva com concavidade para baixo, indicando um crescimento que ia mais devagar a cada passo, e no ponto azul ela passou a ter uma concavidade para cima, indicando um crescimento que vai cada vez mais rápido.
E matematicamente falando, como podemos achar esse ponto? Bom, esse é um ponto crítico onde a segunda derivada da função vale zero. Ou seja
Passo 2
Vamos calcular as duas derivadas:
Lembra que a derivada da soma é o mesmo que a soma das derivadas? Ou seja
Agora vai ser só calcular cada uma dessas derivadas aí. Pra derivada de polinômio temos
Lembrando que a derivada da constante vale zero, certo? Logo a derivada daquele 7 ali vai ser nula...cuidado.
E agora fazemos o mesmo processo pra segunda derivada
Passo 3
Vamos começar achando os pontos que tem derivada segunda igual a zero:
Vamos dividir tudo por pra deixar nossas contas mais simples. Atenção na matemática aqui. Lembra que numa equação, tudo o que fazemos de um lado, temos que também fazer no outro pra mantermos a igualdade, certo? Então
Como é uma equação de segundo grau, podemos usar Bháskara fazendo:
Detalhe, no nosso caso temos
Vamos jogar nas fórmulas então. Primeiro calculando o delta
Ou seja, temos duas raízes:
Passo 4
Beleza, descobrimos as coordenadas dos pontos de inflexão, e pra descobrir as coordenadas vamos jogar esses valores de na função
- Para
- E para
E o primeiro ponto é
E o segundo ponto é .
Prontinho, achamos os pontos de inflexão.
Resposta
Os pontos de inflexão são e .