Reta Tangente
Teoria
As derivadas são importantes por terem diversas aplicações, tanto dentro do cálculo, quanto em outras áreas de estudo. Uma das aplicações mais importantes é o seu uso para encontrar a equação da reta tangente de funções.
Então bora lá que esse vai ser o assunto de hoje!
Mas o que é uma reta tangente?
Primeiro vamos entender o que seria essa tal reta tangente, olhando para o gráfico de uma função :
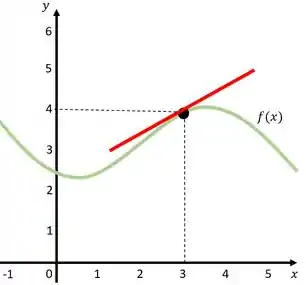
Essa reta vermelha é a nossa reta tangente. Dizemos que ela tange o gráfico da função (em verde) no ponto . Isso quer dizer que ela encosta no gráfico da função exatamente nesse ponto.
O que aconteceria se pegássemos vários pontos diferentes da mesma função? Dá uma olhada:
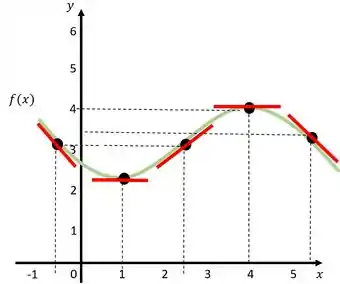
Perceba que pra cada ponto diferente que pegamos no gráfico, temos uma reta tangente diferente também. Isso significa que as retas tangentes são específicas pra uma função e um ponto, então guarda essas duas coisas que vão ser importantes lá na frente!
Outra coisa legal de olhar na imagem é como as tangentes têm um comportamento parecido, a reta se aproxima da função conforme se aproxima do ponto, toca nele e depois se afasta da função de novo. Isso não é uma regra pra todas as tangentes, mas acontece na maior parte dos casos, então já serve como um guia!
Encontrando a equação da reta tangente
Bom, agora que sabemos o que é uma reta tangente, vamos ver como isso se relaciona com as derivadas!
É bastante comum encontrarmos problemas desse tipo:
“Determine a equação da reta tangente ao gráfico da função no ponto .”
Aqui, estamos procurando a equação da reta tangente ao gráfico de uma função em um ponto específico. Pra fazer isso, vamos usar a fórmula da equação da reta, que é essa aqui:

Vamos destacar algumas coisinhas importantes nessa equação:
- são as coordenadas do ponto de tangência entre a reta e o gráfico da função, ou seja, o ponto da função onde queremos encontrar a equação da reta tangente
- é o coeficiente angular da reta, que diz qual a sua inclinação. Ele é exatamente a derivada da função.
Com isso, já temos tudo que precisamos pra resolver nosso exemplo:
“Determine a equação da reta tangente ao gráfico da função no ponto .“
Passo 1: Vamos começar descobrindo o coeficiente angular da reta , que é a derivada da função quando :
Derivando a função :
Para achar substituímos o por na derivada que acabamos de encontrar:
Assim:
Prontinho!
Passo 2: Agora precisamos descobrir as coordenadas do ponto de tangência.
Como estamos falando do ponto que queremos encontrar a equação da reta tangente, o ponto dado será o nosso . Já o , vamos encontrar substituindo o na função:
Assim, e !
Passo 3: Agora, substituímos tudo que encontramos lá na equação da reta tangente:
Passo 4: Pra ficar bem arrumadinho, vamos isolar o e multiplicar o pelos termos entre parênteses, ficando com:
E essa é a equação na reta tangente que estávamos procurando!
Por hoje é só, bora praticar!
Encontrando a equação da reta tangente
Exercícios Resolvidos
Exercício Resolvido #1
O coeficiente angular da reta tangente à curva no ponto é dado por:
Passo 1
Não se assuste com esse tal de “coeficiente angular da reta tangente”! O nome parece difícil, mas a gente já conhece isso com o nome de “derivada”!
Isso porque o coeficiente angular (a inclinação) da reta tangente a uma curva é a derivada da curva no ponto em questão.
Isso mesmo! Na verdade, o que o problema quer saber é a derivada da função no ponto .
Vamos lá então?
Passo 2
Veja que a nossa função é uma fração, então a gente vai usar a Regra do quociente para resolvê-la.
Vamos relembrar como é esse regra?
A regra do quociente é assim:
Onde o ““ representa a derivada.
Passo 3
Como a nossa função é:
Vamos chamar:
e
E essas aqui a gente já aprendeu a derivar, lembra? Derivada de constante é zero, e derivada de potência fazemos com a “Regra do Tombo”. Vai ficar assim:
Passo 4
Agora que já derivamos a função de cima e a debaixo, vamos montar nossa regra do quociente substituindo , , e :
Resolvemos essas multiplicações a gente tem:
Beleza! Achamos nossa derivada! Agora só falta um detalhezinho...
Passo 5
Como a gente quer o coeficiente angular no ponto , vamos calcular nossa derivada no ponto onde , olha só:
E prontinho! Esse é o coeficiente angular no ponto ! 😉
Resposta
O coeficiente angular da reta é .
Exercício Resolvido #2
Dada a função , determine a equação da reta tangente no ponto , marcando a única alternativa correta.
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala aí, tudo joia? Vamos ver mais essa questão de aplicação de derivadas aqui😊
Se queremos a equação da reta tangente, primeiro precisamos achar o seu coeficiente angular. Em outras palavras, primeiro precisamos calcular a derivada de naquele ponto dado. A nossa função é essa aqui:
Como estamos falando de um polinômio, a derivada é feita usando aquela Regra do Tombo em cada termo, lembra? A regra vai ser aplicada a cada potência desse jeitinho aqui:
E vai dicar assim:
(derivada de constante é sempre zero,não esquece😉)
Arrumando ali, nossa derivada é:
Passo 2
Beleza, já achamos a derivada! Mas o enunciado pediu a derivada no ponto , ou seja, vamos fazer na expressão da derivada:
Calculando, teremos:
Show! Achamos o coeficiente angular da nossa reta tangente!
Passo 3
Agora se liga só, a equação da reta tangente tem essa forma aqui:
Onde é o coeficiente angular, e é o ponto de tangência.
Aqui no nosso caso temos que foi o que acabamos de calcular no passo anterior, e . Então, bora jogar isso ali na equação da reta tangente!
Organizando tudo:
Passo 4
Pra ficar no formato direitinho das alternativas, precisamos igualar a zero. Pra isso é só a gente jogar tudo pro mesmo lado, lembrado de mudar os sinais, assim:
Prontinho! Esse é a equação da reta tangente no ponto que está igualzinho a letra (e)! 😄
Resposta
(e)
Exercício Resolvido #3
Escreva a equação da reta tangente ao gráfico da função em .
Passo 1
Fala aí, tudo joia?
Bom, o primeiro passo para completarmos a equação da reta tangente é calcular o coeficiente angular dessa reta. Em outra palavras: calcular a derivada da função no ponto .
Pra isso, vamos derivar a nossa função então.
Lembra que em derivadas de potências a gente usa a Regra do Tombo no expoente. A derivada aqui fica:
(todo número elevado a zero é 1😉)
Beleza, essa é a nossa derivada então!
Passo 2
A gente precisa do valor dessa derivada no ponto , então vamos substituir na derivada que a gente achou...
E pronto! Esse é o coeficiente angular da nossa reta.
Passo 3
Agora a gente vai montar a equação da reta tangente, e ela tem essa forma aqui:
Onde é o coeficiente angular, e é o ponto de tangência.
Show! No nosso caso então temos e .
Vamos substituir isso ali agora...
Passo 4
A equação da reta tangente é:
Jogando tudo para o lado esquerdo:
Prontinho! Essa é a equação da reta tangente ao gráfico de no ponto 😊
Resposta
A equação da reta é .
Exercício Resolvido #4
A função é conhecida como fólio de Descartes. Encontre a equação da reta tangente à função no ponto .
(a)
(b)
(c)
(d)
(e)
Passo 1
Pra encontrar a equação da reta tangente a gente precisa da derivada, que é o coeficiente angular, lembra?
Mas aqui a nossa função não está escrita como de costume, o não está isolado. Quando isso acontece dizemos que temos uma função definida implicitamente. Pois nossa função não tá isolada dessa forma aqui:
Sendo assim, precisaremos derivar implicitamente também, ok?! Como faz isso?
A gente vai derivar cada termo de acordo com cada variável e vai indicar qual a variável que a gente derivou. Vem acompanhando comigo...
Passo 2
Vamos pegar nossa função:
E repartir dessa forma aqui:
A gente vai derivar cada pedacinho desse, e depois remontar nossa equação.
Passo 3
Primeiro essa:
Nossa variável aqui é , então a gente vai derivar normalmente, como a gente já tá acostumado. E aí vamos colocar um na frente, pra identificar que derivamos o :
Beleza, vamos pro próximo pedacinho...
Passo 4
O nosso próximo pedacinho vai ser esse aqui:
Da mesma forma do outro, só que agora a gente tá derivando o então vamos colocar um na frente pra identificar:
Joia! Vamos seguir...
Passo 5
Agora falta esse pedacinho aqui:
Nesse a gente precisa de uma atenção especial, porque temos as duas variáveis. Como temos um produto, a gente aplica a regra do produto aqui, que é:
Vamos chamar aqui:
E aqui derivando a gente tem:
Então...
Passo 6
Beleza, já derivamos cada pedacinho, agora vamos voltar pra nossa equação...
Substituindo as derivadas de cada termo:
Agora vamos agrupar tudo o que tem de um lado e tudo o que do outro:
Agora vamos passar o dividindo pro lado do :
E vai pro outro lado também dividindo:
Beleza! E assim encontramos a derivada da função! Ufaa...
Passo 7
Agora, a gente vai ver o valor dessa derivada no ponto pedido substituindo o por e o também por .
Show! Esse é o coeficiente angular da reta!
Passo 8
A equação da reta tangente é da forma:
Onde é o coeficiente angular e é o ponto de tangência.
No nosso caso, e .
Substituindo, vamos ter:
E então chegamos na reta tangente! A resposta é a letra D😉
Resposta
(d)
Exercício Resolvido #5
Considerando que a função custo de determinada mercadoria é expressa por:
Podemos afirmar que a função custo marginal será expressa por:
(a)
(b)
(c)
(d)
(e)
Passo 1
Essa aqui tem uma carinha diferente, mas tem uma resolução bem parecida com as anteriores!
A função “custo marginal” é simplesmente a derivada da função do custo. Ou seja, se a gente derivar a função do custo vamos encontrar nossa função custo marginal!😊
Vamos lá então?
Passo 2
A função do custo é um polinômio, então a gente derivar cada termo e conservar a soma. Pra derivar cada termo, vamos usar a Regra do Tombo no expoente, que é essa aqui:
Vai ficar assim:
Lembra que derivada de constante é zero, e que todo número elevado a zero é 1:
E assim, encontramos nossa derivada e, consequentemente, nossa função de custo marginal! 😚
Resposta
(a)
Exercício Resolvido #6
Determine o ponto crítico da função
- 3 e 4
- Nenhuma das respostas anteriores
- 2 e 3
- 3
- 0
Passo 1
Fala aí, tudo beleza? Essa aqui é outra aplicação das derivadas!
Vamos encontrar um ponto crítico da função, que é um ponto bem especial.
A derivada representa a inclinação da reta tangente ao gráfico em determinado ponto. Chamamos de ponto crítico, um ponto que pode ser de máximo, ou de mínimo da nossa função. Nesses pontos a reta tangente fica na horizontal e não tem inclinação, com isso a derivada será igual a zero.
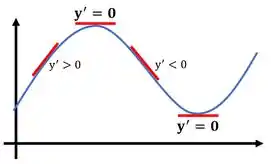
Por hora, vamos aprender a calcular esse ponto...
Então para determinarmos o ponto crítico, vamos encontrar a primeira derivada da nossa função e depois igualar ela a zero, vamos lá?
Passo 2
Nossa função é:
A gente deriva com a regra do Tombo, que a gente já aprendeu lá atrás, descendo o expoente pra frente e perdendo 1 no novo expoente. Vai ficar assim:
Como todo número elevado a zero é 1...
Essa é a nossa derivada!
Passo 3
Agora vamos igualar a derivada que achamos a zero ...
Prontinho! Esse é o nosso ponto crítico da função. Quer dizer que ele pode ser um ponto de valor máximo ou de valor mínimo! Como não sabemos qual dos dois, chamamos apenas de ponto crítico. 😉
Resposta
d) 3.
Exercício Resolvido #7
Determine qual(is) são os pontos críticos da função .
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala aí, tudo joia?
Olha só, ponto crítico é onde a derivada é zero, beleza?
Isso porque a derivada é a inclinação da reta tangente ao gráfico. Um ponto crítico é um ponto onde a função atinge seu valor máximo ou mínimo, nesses pontos a reta tangente fica completamente na horizontal. Sendo assim, ela não terá nenhuma inclinação, e por isso a derivada será igual a zero.
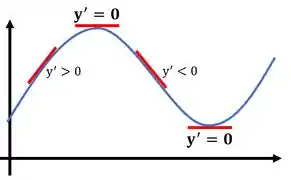
Vamos começar calculando a derivada então...
Passo 2
Vamos derivar essa função aqui:
A gente tem um polinômio, então vamos derivar usando a regra do Tombo, lembra dela?
Vamos aplicar isso na nossa função!
Passo 3
Aplicando a regra do Tombo na função , temos:
A gente ainda pode colocar o em evidência:
Passo 4
Agora que já achamos a derivada, vamos ver em que ponto ela é igual a zero, fazendo:
Pra um produto dar zero, um dos fatores tem que ser zero, como aqui temos o multiplicando o , podemos ter essas duas condições:
Resolvendo essa segunda equação...
Passo 5
Beleza! Achamos os dois pontos críticos então, que são:
E é só isso por aqui😊
Resposta
(d)
Exercício Resolvido #8
Seja . Determine o(s) intervalos onde a função é decrescente
(a)
(b) Nenhuma das respostas
(c)
(d)
(e)
Passo 1
Opa! Tudo joia?
Olha só: uma função é decrescente nos pontos em que a sua derivada é negativa. Isso porque a derivada representa a inclinação da reta tangente a função. Quando o gráfico de uma função está descendo a reta tangente a ele estará inclinada negativamente. Veja o exemplo desse gráfico aqui:

Vamos achar a derivada de então!
A gente vai usar a regra do Tombo, beleza?
Essa aqui:
Passo 2
Aplicando essa regra na nossa função, fica assim:
(Lembra que derivada de constante é zero e que 😊)
Passo 3
A gente quer os pontos onde a derivada é negativa, ou seja:
Vamos resolver essa inequação, então!
Passo 4
Pra finalizar, dividimos esse módulo em positivo ou negativo:
Como nessa segunda temos um , pra deixá-lo positivo, nós multiplicamos tudo por , o que no final das contas, vai mudar o sinal de todo mundo, incluindo o sinal de que vai virar :
Com isso, temos que:
( é maior que )
( é menor que
Com isso, o intervalo onde a derivada é negativa é:
E esse é o intervalo onde a função é decrescente! 😊
Resposta
Letra (c).
Exercício Resolvido #9
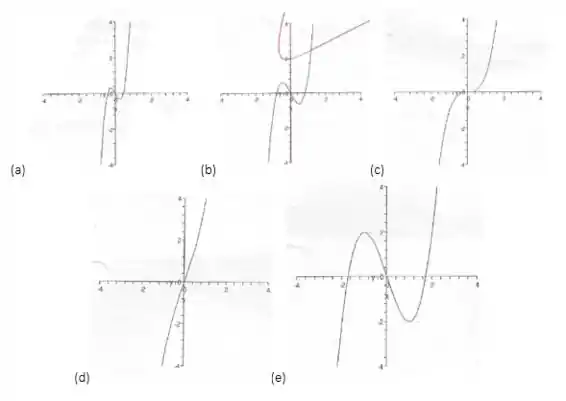
Aplicando os conceitos de derivada, qual o gráfico da função definida em por ?
Passo 1
E aí, tudo beleza?
Vamos ver qual é o gráfico dessa função aqui:
Bom, o exercício falou pra a gente usar os conceitos de derivada. A gente sabe que com a derivada podemos achar os pontos de máximo e mínimo da função, bem como os intervalos de crescimento e decrescimento. Bora lá então?
Passo 2
Bora derivar a função então! A gente vai usar a regra do Tombo: .
Aplicando em :
Passo 3
Bom, os pontos críticos da função, que são nossos candidatos a ponto de máximo e mínimo são os pontos onde a derivada é zero. Vamos ver isso igualando a derivada que acabamos de encontrar a zero, então:
Beleza! Esses são os pontos críticos da função😊
Passo 4
Vamos ver o valor da função nesses pontos agora. É só substituir os pontos na expressão da função. Um de cada vez e a gente vê qual o resultado:
Olha só! Quando substituímos o nossa função deu , e quando substituímos o , nossa função de . Assim concluímos que temos um ponto de mínimo em e um ponto de máximo em !
Isso só acontece lá no último gráfico, na letra , que é o gráfico da nossa função😉
Resposta
Letra (e).
Exercício Resolvido #10
Algumas das aplicações mais importantes do cálculo diferencial são os problemas de otimização, em que devemos encontrar a maneira ótima (melhor maneira) de fazer alguma coisa. Um bom jeito de achamos essa maneira é avaliando os pontos de máximo e mínimo da função que descreve nosso problema.
Encontre os máximos e mínimos relativos da função .
Passo 1
E aí, tudo bem?
Aqui a primeira coisa que vamos fazer, é derivar essa nossa função e depois igualar a nossa a zero para determinarmos os pontos críticos dela:
Usamos a regra do Tombo aqui: :
Passo 2
Vamos igualar essa nossa a zero
Pra resolver essa equação do segundo grau, vamos utilizar a fórmula de Bháskara:
Sendo que aqui temos: :
Passo 3
Encontramos as coordenadas de dos nossos pontos críticos.
Agora nos resta descobrir quem é mínimo e quem é máximo. Substituindo esses valores em e comparando os valores encontrados poderemos descobri quem será o máximo e quem será o mínimo:
Substituindo o ;
Passo 4
E agora substituindo o :
Passo 5
O nosso maior valor de , vai nos dar o ponto de máximo:
O nosso menor valor de , vai nos dar o ponto de mínimo
E fechamos! 😊
Resposta
Exercício Resolvido #11
Encontre os pontos de inflexão da curva .
Passo 1
Pra ter uma ideia do que estamos falando, um ponto de inflexão é uma coisa como essa:
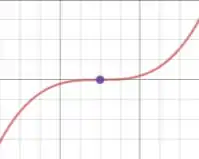
Pondemos dizer que é o ponto onde a função muda de comportamento. Repara que ela tinha uma cruva com concavidade para baixo, indicando um crescimento que ia mais devagar a cada passo, e no ponto azul ela passou a ter uma concavidade para cima, indicando um crescimento que vai cada vez mais rápido.
E matematicamente falando, como podemos achar esse ponto? Bom, esse é o ponto onde a segunda derivada da função vale zero. Tranquilo, né? Ou seja
Passo 2
Vamos calcular as duas derivadas:
Lembra que a derivada da soma é o mesmo que a soma das derivadas? Ou seja
Agora vai ser só calcular cada uma dessas derivadas aí. Pra derivada de polinômio temos
Lembrando que a derivada da constante vale zero, certo? Logo a derivada daquele 7 ali vai ser nula...cuidado.
E agora fazemos o mesmo processo pra segunda derivda
Vamos começar achando os pontos que tem derivada segunda nula, ou seja
Vamos dividir tudo por pra deixar nossas contas mais simples. Atenção na matemática aqui. Lembra que numa equação, tudo o que fazemos de um lado, temos que também fazer no outro pra mantermos a igualdade, certo? Então
Como é uma equação de segundo grau, podemos usar Bháskara fazendo:
Detalhe, no nosso caso temos
Vamos jogar nas fórmulas então. Primeiro calculando o delta
Ou seja, temos duas raízes:
Passo 3
Beleza, descobrimos as coordenadas dos pontos de inflexão, e pra descobrir as coordenadas vamos jogar esses valores de na função
- Para
- E para
E o primeiro ponto é
E o segundo ponto é .
Prontinho, achamos os pontos de inflexão.
Resposta
Os pontos de inflexão são e .
Exercício Resolvido #12
Um pedaço de papel retangular é usado para construir uma caixa sem tampa, pra isso corta-se quadrados iguais de cada canto do papel. O papel retangular possui 8 centímetros de largura por 15 centímetros de comprimento. Determine o volume máximo para tal caixa.
- Aproximadamente 90,74;
- Exatamente 60;
- Aproximadamente 80;
- Aproximadamente 50;
- Nenhuma das respostas anteriores.
Passo 1
Vamos pensar no nosso retângulo, o enunciado nos mostra que ele é assim ó
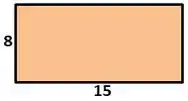
O enunciado nos disse que ele vai recortar quadrados nos quatro cantos, então teremos o seguinte:
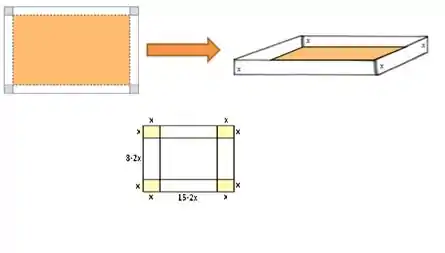
O volume dessa caixa, será:
Se você for observar bonitinho aquele desenho, vai ver que a altura vale , certo? A largura dela vale e o comprimento vale , então agora é substituir isso aí na nossa fórmula do volume.
Resolvendo as multiplicações, teremos:
Passo 2
Como ele pediu o maior volume possível da caixa, teremos que achar o valor máximo da função volume.
Para encontrarmos os pontos de máximo e mínimo, vamos fazer a primeira derivada e igualar ela a zero! Grava isso...máximo e mínimo, primeira derivada igual a zero
Derivando, teremos:
Observa que a derivada da soma é igual a soma das derivadas, certo? Então
Observa que deixei todas as constantes de fora da derivada.
Agora é só derivar tudo aí. Vamos lembrar a derivada de polinômio?
Então
Agora vamos igualar isso a zero e encontrar as raízes
Resolvemos essa equação do segundo grau pra ver onde que ela vale zero. Primeiro vem nosso delta
Detalhe, no nosso caso temos
Vamos jogar nas fórmulas, então. Primeiro calculando o delta
Ou seja, temos duas raízes:
Beleza, agora precisamos ver qual das duas nos dá o maior e o menor volume possível...
Vamos substituir esses valores na expressão que encontramos para o volume, essa aqui ó:
Primeiro o
Fazendo o
Esse obviamente, vamos descartar porque não faz sentido termos um volume negativo!
Sendo assim, o volume é proximo de ! Letra A!
Resposta
Letra A
Exercício Resolvido #13
Quando um prato circular de metal é aquecido em um forno, seu raio aumenta a uma taxa de 0,01 cm/min. A que taxa a área do prato aumenta quando seu raio é de 50 cm?
Passo 1
Temos pelo enunciado que a taxa de variação do raio de um prato em relação ao tempo é de que isso significa? Simplesmente que a primeira derivada da função vale. Tranquilo demais, né? Então
Sabemos que para determinarmos a área de um prato circular teremos
Lembra que é assim que representamos a área de algo circular. Onde esse é o tamanho do raio do prato.
Observa que o que está variando com o tempo é o raio, certo? Então é nossa variável. Teremos então
Lembre que varia em relação a , então vamos fazer uma derivação implícita.
Como temos
Poderemos escrever o seguinte
Resposta
Exercício Resolvido #14
Uma pessoa dispõe de 900m de arame para cercar um terreno retangular. Utilizando o conceito de derivada, determine as dimensões deste terreno para que o mesmo apresente área máxima.
Passo 1
Beleza, a princípio temos um terreno com a seguinte cara:
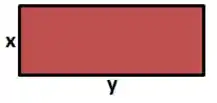
O que o problema quer que a gente descubra, são os valores de e de que fazem com que ele tenha a maior área possível. Então vamos descobrir quem é a função que descreve a área e encontrar os valores de e de que fazem seu valor ser máximo, pra isso usaremos os conceitos de derivada que estamos estudando.
O enunciado nos afirma que o cercado em preto é de 900 metros. Ou seja, o seu perímetro é
Podemos simplificar essa expressão, dividindo tudo por . Isso vai facilitar os nossos cálculos mais à frente.
Podemos isolar o e ficamos com
Dessa forma, as dimensões do terreno serão
Agora vamos falar sobre a área desse terreno. Ela é a multiplicação de um lado pelo outro, certo? Então
Prontinho, achamos a função que descreve a área desse terreno.
Passo 2
Para encontrarmos a maior área possível, vamos procurar o valor máximo da função área que a gente acabou de encontrar no passo anterior. Pra isso precisamos fazer a primeira derivada dela e depois igualar a zero. Lembra que pra acharmos os valores de máximos e mínimos nós fazemos a primeira derivada igual a zero? Então...isso que faremos agora.
Mãos a obra...
Achamos a derivada. Agora vamos igualar a zero e encontrar o valor de nesse ponto....
Agora vamos atrás do valor de .
Como vimos antes
Ou seja, esse nosso retângulo será na verdade um quadrado com lado , tendo a maior área possível de ser cercada com a quantidade de arame disponível.
Resposta
Quadrado com lado
Exercício Resolvido #15
Uma partícula se move sobre uma linha reta de modo que, após de segundos, sua distância em metros do ponto de partida seja dada por . Indique a velocidade da partícula no instante em que segundos:

(a)
(b)
(c)
(d)
(e)
Passo 1
Fala aí! Tudo bem?
Achou estranha essa questão estar aqui em cálculo? Mas não se espante, é isso mesmo! Aqui temos mais uma aplicação de derivada!
É o seguinte: a velocidade da partícula é dada pela derivada da posição dela em relação ao tempo!
Ou seja:
Passo 2
Aqui no nosso caso, a posição é:
A velocidade então é dada pela derivada dessa função em relação a ! Ou seja:
A gente vai derivar usando nossa regra do Tombo:
Passo 3
Jogando na nossa função, temos:
Show! Essa é a função da velocidade😊
Passo 4
Como queremos a velocidade no instante , vamos substituir:
E a velocidade é dada por , então:
Alternativa (d) 😉
Resposta
(d)
Exercício Resolvido #16
Um fazendeiro tem m de cerca e quer cercar um campo retangular que está na margem de um rio reto. Ele não precisa cercar o lado do terremo que ficará a margem do rio. Quais são as dimensões que ele deve usar para obter um campo com a maior área possível, podendo ser cercando com a quantidade de cerca disponível?
(a) por
(b) por
(c) por
(d) por
(e) por
Passo 1
E aí, tudo beleza?
Dá uma olhadinha no desenho aqui pra entender melhor:
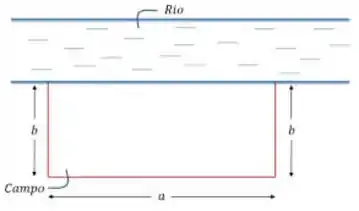
Ali temos o campo, de lados sendo que em um dos lados medindo temos a margem do rio.
Queremos saber quais sãos os valores de , nessas condições, para que o campo tenha área máxima. Vem comigo!
Passo 2
A questão nos disse que o fazendeiro tem de cerca, e a quantidade de cerca de um campo retangular é dado pelo perímetro (soma dos lados) dele.
Nesse caso vamos somar os lados com exceção do lado à margem do rio. Temos:
Como temos de cerca, nosso perímetro deverá ser:
Vamos colocar e função de :
Ok, encontramos uma relação entre os dois lados do campo. Guarda isso por enquanto!
Passo 3
A gente quer encontrar a área máxima, sendo que área do campo é dada por:
Mas, a gente achou ali em cima que:
Bora jogar isso no lugade de na expressão da área, então?
Fazendo a distributiva...
Encontramos a expressão da área em função de 😊
Passo 4
Como queremos encontrar a maior área possível, vamos maximizar essa função:
Pra achar o ponto máximo dela, vamos encontrar onde a derivada dá zero. Vamos derivar usando a regra do Tombo:
Passo 5
Ótimo! Agora vamos ver onde essa derivada zera:
Show! Achamos o valor de que faz com que a área seja máxima!
Passo 6
Pra achar o valor da dimensão é mais fácil, porque a gente já viu que:
E como , temos:
Show de bola!
Então para que tenha área máxima, nessas condições, o campo deve medir por 😉
Alternativa (d)!
Resposta
Letra (d)
Exercício Resolvido #17
Se de material estiverem disponíveis para fazer uma caixa com uma base quadrada e sem tampa, encontre o maior volume possível da caixa.
(a)
(b)
(c)
(d)
(e) Nenhume das alternativas
Passo 1
E aí, tudo bem?
A gente quer uma caixa mais ou menos assim:
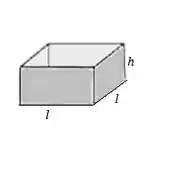
Já que a base é quadrada.
O enunciado também nos deu que estão disponíveis de material para fazer essa caixa.
A nossa restrição então é que a área total dela é 1200.
Vamos colocar em linguagem matemática...
Passo 2
A área total dessa caixa é dada pela soma das áreas de cada pedacinho.
Temos a base, que é:
E temos 4 laterais retangulares, medindo por , ou seja:
A área total vai ser a soma da área da base mais as áreas laterais. Então ela será dada por:
E como a área total é 1200, temos:
Ok, segura isso por enquanto!
Passo 3
Vamos lá, a gente quer encontrar o maior volume possível pra caixa, dentro da condição que a gente viu ali em cima.
O volume da caixa (que é um paralelepípedo) é calculado assim:
Vamos colocar isso em função de uma variável só usando a condição que achamos ali em cima.
Passo 4
A gente pode isolar o nessa aqui pra deixar em função de :
Vamos substituir na fórmula do volume agora:
Simplificando o :
Passo 5
Beleza, agora que temos a função a ser maximizada em termos de uma variável só. Podemos partir para a derivada, e ver os pontos onde essa deriva é igual a zero.
Passo 6
Ok, agora é só acharmos o valor de que acompanha esse e depois calcular o volume!
E então o volume máximo possível é:
Alternativa (a) 😊
Resposta
Letra (a).
Exercício Resolvido #18
Em muitas situações do trabalho, é necessário o entendimento entre os relacionamentos do lado, da área ou volume de um ambiente. Sabemos que a área (A) do quadrado é L². Se o lado (L) de um quadrado aumentar 5%, qual será o aumento aproximado da área (A) deste quarado?
Passo 1
Opa! Vamos ver mais esse aqui?
A gente quer saber o que acontece com a área do quadrado se aumentarmos o lado em . Vamos ver isso...
Como não sabemos o lado do nosso quadrado, vamos dizer que ele mede .
Sendo assim, a área do quadrado será
Beleza, vamos seguir...
Passo 2
Se a nosso lado aumentar em 5% isso significa que passará a valer:
Isso porque, ele tem um tamanho inicial que é representado por , ao aumentarmos , ela vai para , que é na verdade
(Lembre-se que )
Ou seja...
Nossa nova área será
Passo 3
Desse modo, o aumento será de:
Jogando isso pra porcentagem (multiplica por 100), temos:
Prontinho! Vemos então que a área aumenta bem mais que o lado! 😉
Resposta
Exercício Resolvido #19
Certo lago pode suportar uma população máxima de peixes. Considerando que há poucos peixes no lago, sabe-se que a taxa de crescimento populacional será proporcional ao produto da população existente pela diferença da população existente a partir de , ou seja, , onde é a taxa de crescimento para uma população de dimensão .
Pergunta-se: Para que população a taxa de crescimento será máxima?
Passo 1
E aí, tudo beleza?
Aqui a pergunta é: qual o valor de que maximiza a função:
Sabemos que para fazer essa maximização, precisamos procurar o ponto crítico de , ou seja, o ponto onde a derivada é zero.
Vamos derivar essa função então pra começar...
Passo 2
Primeiro multiplicando os termos ali pra ficar mais fácil:
Vamos derivar agora, sendo constante:
Passo 3
O ponto crítico é onde a derivada é zero, então:
Como é constante e está nos dois termos, podemos cortar
Ficando com:
Passo 4
E podemos confirmar que isso é um ponto de máximo se verificarmos que a derivada segunda é negativa:
Ótimo, então de fato temos um máximo na taxa quando 😊
Resposta
A taxa de crescimento é máxima quando a população é de peixes.