Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.6 - Ex. 45
45 - Nos Exercícios 45 e 46, use um teorema de Pappus para determinar o centroide do triângulo dado. Use o fato de que o volume de um cone de raio r e altura h é V = .
Passo 1
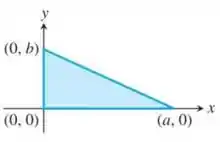
Analisando a figura temos que rario r = a e altura h = b
Utlizando o teorema de Pappus teremos:
Assim:
Agora pelo eixo x:
Assim:
Resposta
Exercícios de Livros Relacionados
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos. y = s e nx ,y = cos
Encontre uma integral para o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas sobre a reta especificada. Em seguida, use a calculadora para determinar a integral com precis
Cada integral representa o volume de um sólido. Descreva o sólido. π ∫ - 1 1 ( 1 - y 2 )d y
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos. y = 1 - x 2 ,y = 0 ;
Encontre uma integral para o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas sobre a reta especificada. Em seguida, use a calculadora para determinar a integral com precis