Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.3 - Ex. 73
69-73. A noção de assíntota pode ser estendida para incluir curvas não necessariamente retas. Especificamente, dizemos que as curvas e são assintóticas quando se:
E assintóticas quando se:
Nesses exercícios, determine uma função mais simples, tal que seja assintótica a quando ou . Use um recurso gráfico para gerar os gráficos de e de e identifique todas as assíntotas verticiais.
73.
Passo 1
Então galera, como deve ser assintótica, vamos chamar:
Utilizando o limite que o enunciado nos indica, teremos:
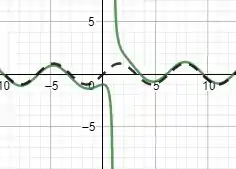
Sendo assim, podemos concluir que é assintótica para . Ademais, só há uma assíntota vertical no gráfico da função, que é em . Plotando isso, teremos:
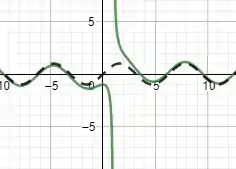
No qual a função em verde é e a função pontilhada é .
Resposta
Assíntota Vertical:
Exercícios de Livros Relacionados
Calcule os limites aplicando os limites fundamentais. lim x → 2 10 x - 2 - 1 x - 2
Calcule os limites aplicando os limites fundamentais. lim x → 0 6 x - s e n 2 x 2 x + 3 s e n 4 x
Calcule os limites aplicando os limites fundamentais. lim x → 0 s e na x s e nb x
Calcule os limites aplicando os limites fundamentais. lim x → 0 s e n 9 x x
Calcule os limites aplicando os limites fundamentais. lim x → 0 t ga x x