Ache as assíntotas horizontal e vertical do gráfico de , determinando o seguinte:
Os extremos relativos de ;
Os pontos de inflexão do gráfico de ;
Os intervalos em que é crescente
Os intervalos em que é decrescente;
Onde o gráfico é côncavo para cima;
Onde o gráfico é côncavo para baixo;
A inclinação de qualquer tangente de inflexão;
As assíntotas horizontal, vertical e oblíqua, se existirem
Passo 1
Primeiramente, vamos observar que essa função é racional. Então quando o denominador for , esse número não estará na função
Isso é importante porque, fora na assíntota vertical, não vamos ter nada rolando nesse ponto. Temos sempre que tirá-lo das análises.
Agora olharando as assíntotas:
Vamos começar pela assíntota horizontal.
Assíntota horizontal: fazer o limite no infinito. Ou seja,
Vamos calcular esses limites. Como temos um polinômio, temos que fazer aquele passo a passo para fração de polinômios, só que para aquela expressão só. Vamos ver como vai ficar isso.
Passo 2
Nosso numerador é
Colocando o em evidência:
Passo 3
Nosso denominador é
Colocando em evidência, vamos ter:
Passo 4
Agora vamos aos limites. Primeiro:
Vai ficar:
Então não temos assíntota horizontal desse lado.
Passo 5
O outro vai ser:
Vai ficar:
Então não temos assíntota horizontal desse lado.
Passo 6
Agora vamos para as assíntotas oblíquas. Só vamos fazer essas assíntotas se não existirem as horizontais. Elas substituem as horizontais por cada lado.
Se as assíntotas horizontais não existirem, talvez existir a oblíqua. Para isso, devemos achar os coeficientes e de que é a equação da assíntota obliqua.
Para isso, devemos fazer
Se esse valor existir, aí fazemos
Mesma coisa para o
Se esse valor existir, aí fazemos
Passo 7
Para acharmos a derivada, vamos usar a regra do quociente:
Passo 8
Nosso numerador é
Colocando o em evidência:
Passo 9
Nosso denominador é
Colocando em evidência, vamos ter:
Passo 10
Agora vamos aos limites. Primeiro:
Vai ficar:
Então temos assíntota oblíqua desse lado.
Vamos achar o valor de
Passo 11
Colocando os valores:
Aqui já temos a fatoração do , e o não percisa fatorar. Entretando o vai ficar:
A assíntota oblíqua para vai ser:
Passo 12
O outro vai ser:
Vai ficar:
Vamos achar o valor de
Passo 13
Colocando os valores:
Aqui já temos a fatoração do , e o não percisa fatorar. Entretando o vai ficar:
A assíntota oblíqua para vai ser:
Passo 14
Vamos para as verticais. Para isso, temos que procurar algum valor de que faça o limite ir para . Normalmente procuramos quando o denominador da fração for . Que vai ser o nosso
Que já achamos. Precisamos analisar a assíntota antes e depois do para ver se de fato temos assíntotas verticais.
E
Passo 15
Opa, deu um número divido por , então ele vai dar , é uma assíntota vertical. Cabe agora descobrir o sinal para o esboço do gráfico.
O denominador é sempre positivo, porque é a soma de um número ao quadrado com .
Como estamos pegando o limite pela direita, ou seja, por valores maiores que , vai ser positivo.
A nossa fração será positiva, então
Então
É assíntota vertical
Passo 16
Opa, deu um número divido por , então ele vai dar , é uma assíntota vertical. Cabe agora descobrir o sinal para o esboço do gráfico.
O denominador é sempre positivo, porque é um número ao quadrado somado de .
Como estamos pegando o limite pela esquerda, ou seja, por valores menores que , vai ser negativo.
A nossa fração será negativa, então
Então
É assíntota vertical.
Passo 17
Vamos aos extremos e os intervalos de crescimento e decrescimento. Para isso temos que analisar o sinal de .
Como o denominador é sempre positivo, basta olharmos o sinal de , que é uma função de grau.
Entre as raízes, vamos ter a derivada negativa, e antes ou depois ela vai ser positiva.
Vamos achar as raízes:
Podemos tirar o da raiz e ficar com
Simplificando
Assim:
Mas porque separamos no ? Lembra lá no inicio que vimos que ele não está na função? Então de lá para frente devemos tirá-lo da conta de tudo, menos assíntota vertical.
A função é crescente se e decrescente se , então:
Passo 18
Agora vamos ver os extremos. Pelo teste da primeira derivada, teremos máximo quando a função vai de crescente para decrescente, e mínimo quando a função for de decrescente para crescente.
Pelos intervalos do passo anterior, vamos ter
Passo 19
Vamos agora para a concavidade e os pontos de inflexão. A função é côncava para cima se e côncava para baixo se .
O ponto vai ser de inflexão quando muda a concavidade.
Para acharmos a derivada, vamos usar a regra do quociente:
Colocando em evidência no numerador:
Simplificando
O sinal depende só de , então
Assim
Então:
Isso também nos diria que é ponto de inflexão, mas ele não está na função. Então não temos ponto de inflexão.
Passo 20
Para terminar vamos ao esboço. Para isso, precisamos juntar todas as informações.
- Assíntota oblíquoa:
- Assíntota vertical
- Assíntota oblíquoa:
- Assíntota vertical
Tanto por quanto
Por , , por ,
Vamos para o gráfico, ele vai ficar assim:
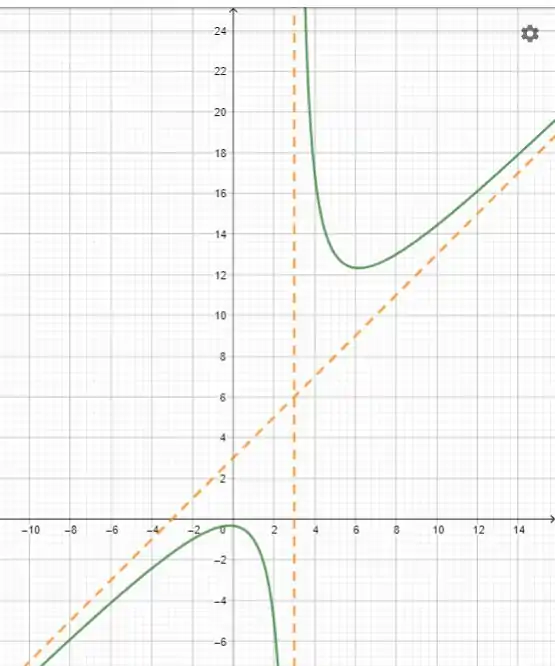
Resposta
Tanto por quanto
Por , , por ,
Vamos para o gráfico, ele vai ficar assim:
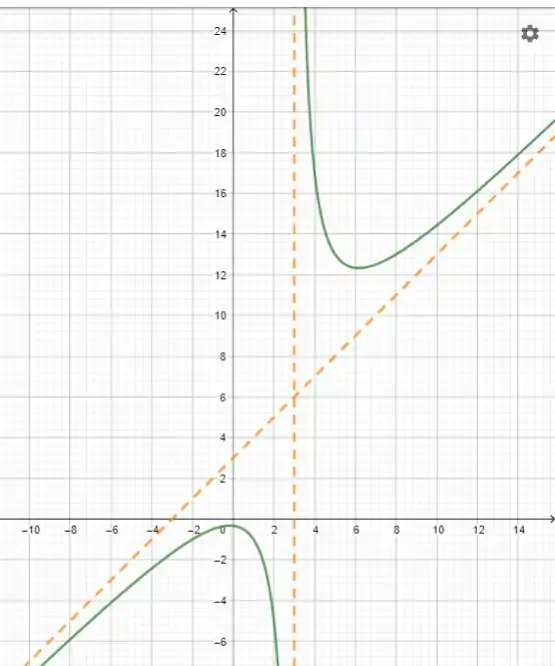
Resposta
Ei, a resposta está no passo a passo :)