5 -
Passo 1
Considere o sistema:
a)
Vamos assumir como a solução do sistema. Portanto iremos substituir esse valor no sistema.
Passo 2
Os valores são as raízes da equação.
Portanto, os autovalores são e .
Passo 3
Quando , a equação fornece,
Cada linha gera a condição:
O autovetor correspondente ao autovalor é:
Passo 4
Encontre o autovetor correspondente ao autovalor .
Substitua na equação ,
Cada linha gera a condição:
O autovetor correspondente ao autovalor é:
Portanto, a solução geral é,
Onde e são constantes arbitrárias.
Passo 5
b) O objetivo é classificar o ponto crítico quanto ao tipo e determinar se ele é estável, assintoticamente estável ou instável.
Os autovalores são números complexos e de sinais opostos. Portanto, o ponto crítico é um espiral. Como a parte real é um real negativo, deve ser assintoticamente estável.
Além disso, todas as soluções se aproximam à medida que t aumenta.
Assim, o ponto crítico é um ponto espiral assintoticamente estável.
Passo 6
c) Várias trajetórias no plano de fase são mostradas abaixo.
E algumas trajetórias terão alguns valores de constantes .
Agora, o esboço das trajetórias é mostrado abaixo:
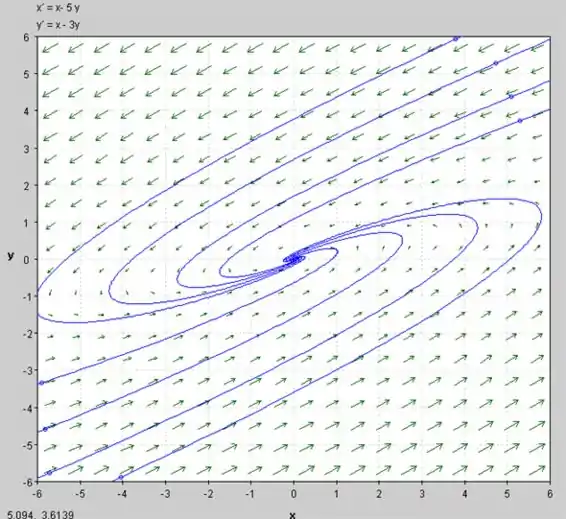
Passo 7
d) O objetivo é usar um computador para plotar com precisão as curvas solicitadas na parte (c).
Digite pplane8 na janela de comando do MATLAB; insira as equações e pressione o botão ENTER para obter os seguintes gráficos:
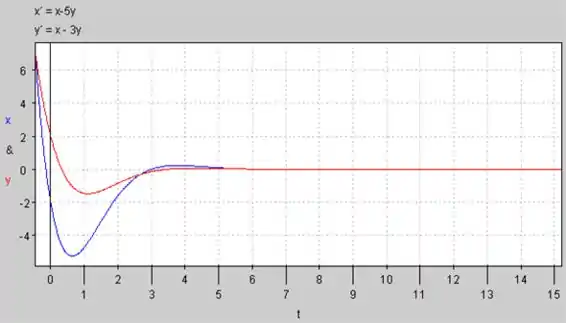
Alguns gráficos típicos de versus para várias condições iniciais são desenhados abaixo:
Para
Gráfico de versus para :
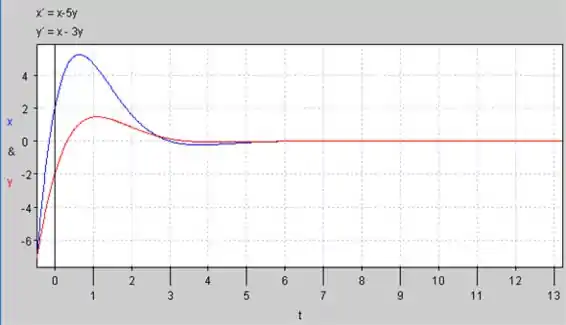
O Gráfico de versus para :
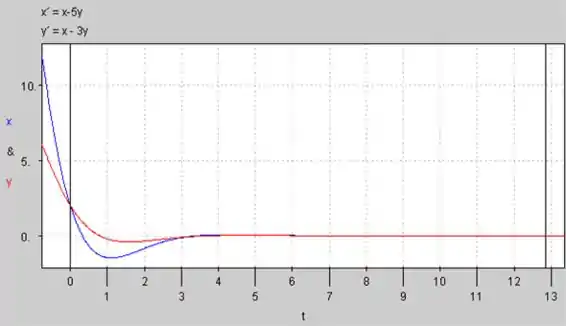
O Gráfico de versus para :
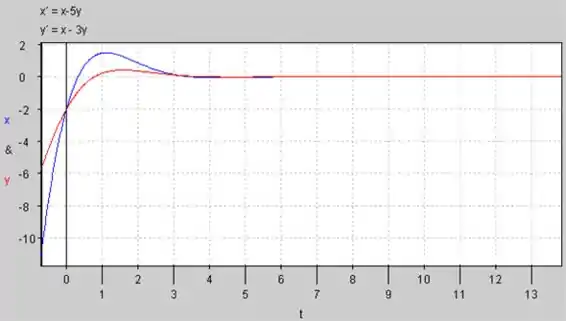
O Gráfico de versus para :
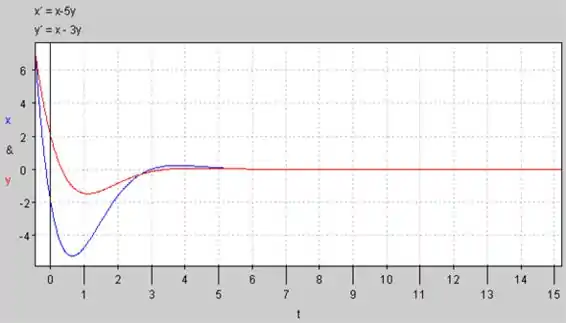
Resposta
- Os autovalores são e .
- O ponto crítico é um ponto espiral assintoticamente estável.
-
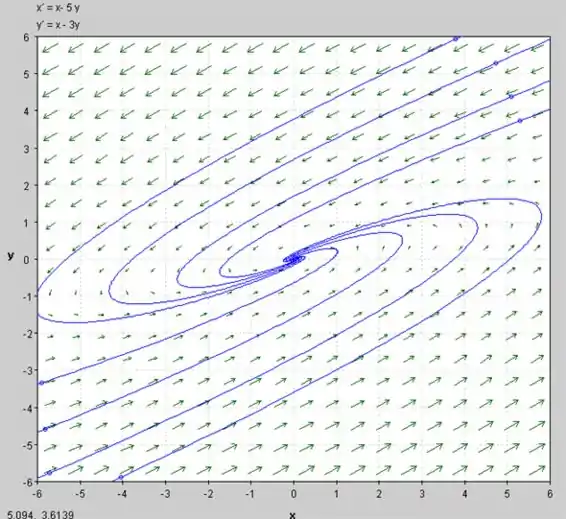
- Gráfico de versus para :
O autovetor correspondente ao autovalor é:
O autovetor correspondente ao autovalor é:
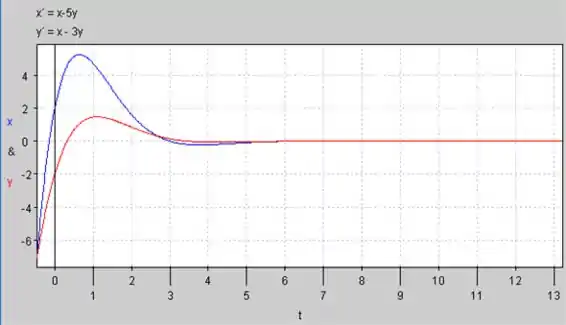
O Gráfico de versus para :
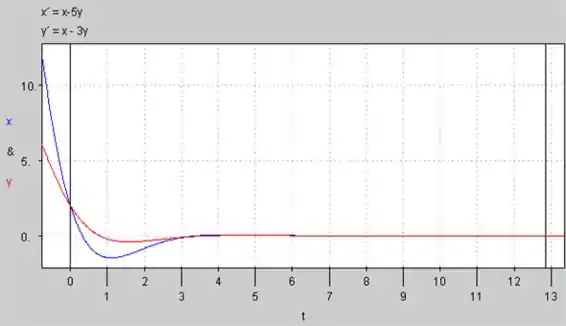
O Gráfico de versus para :
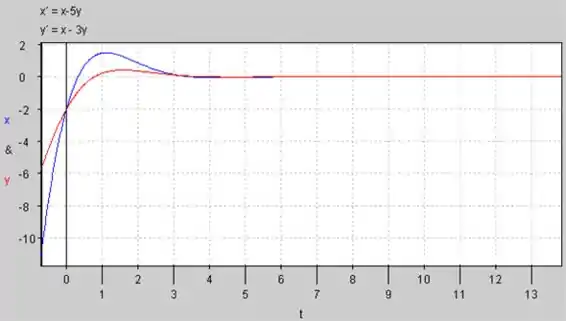
O Gráfico de versus para :