Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.9 - Ex. 1

Calcular o volume do tetraedro da Figura 8.32.

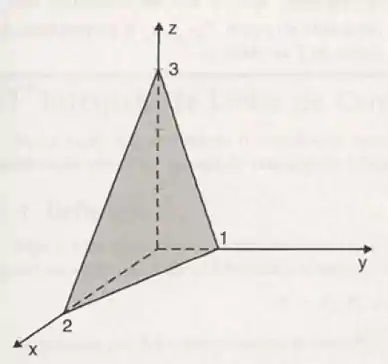
Passo 1

Bora começar?!

Então galera, a primeira coisa a fazer aqui é descobrir qual a equação do plano.

Olhando pela figura nós já podemos inferir que ela será:

(x)/(2) + (y)/(1) + (z)/(3) = 1

Vamos confirmar desenhando?

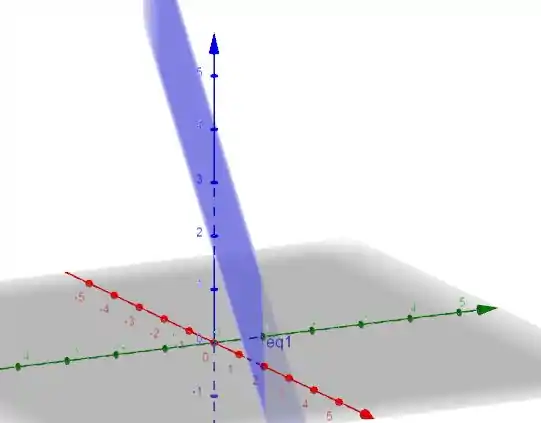
Certinho, não é?

Sendo assim, z é limitada pelo zero e pelo plano:

(z)/(3) = 1 - (x)/(2) - y

z = 3 - (3)/(2) x - 3 y

Então:

0 <= z <= 3 - (3)/(2) x - 3 y

Analisando o x nós vemos que ele também vai do zero até o plano e será máximo quando z = 0 :

(x)/(2) = 1 - y

x = 2 - 2 y

Então:

0 <= x <= 2 - 2 y

Para finalizar nós precisamos do y, e ele vai até seu coeficiente:

0 <= y <= 1

Passo 2

Agora que já sabemos os intervalos de integração:

∭_T^() d V = = ∬_R^() [int_0^(3 - (3)/(2) x - 3 y) d z] d x . d y

Resolvendo:

int_0^(3 - (3)/(2) x - 3 y) d z = z = 3 - (3)/(2) x - 3 y

Sendo assim:

= ∬_R^() (3 - (3)/(2) x - 3 y) d x . d y

= int_0^1 [int_0^(2 - 2 y) (3 - (3)/(2) x - 3 y) d x] d y

Resolvendo a integral:

int_0^(2 - 2 y) (3 - (3)/(2) x - 3 y) d x = 3 x - (3)/(2) (x^2)/(2) - 3 y x

= 3 ( 2 - 2 y ) - (3)/(4) (2 - 2 y)^2 - 3 y ( 2 - 2 y )

= 6 - 6 y - (3)/(4) (4 - 8 y + 4 y^2) - 6 y + 6 y^2

= 6 - 6 y - 3 + 6 y - 3 y^2 - 6 y + 6 y^2

= 3 - 6 y + 3 y^2

Então:

= int_0^1 [3 - 6 y + 3 y^2] d y = 3 y - 6 (y^2)/(2) + 3 (y^3)/(3)

= 3 y - 3 y^2 + y^3

Aplicando o intervalo:

= 3 xx 1 - 3 xx 1^2 + 1^3

= 1

Finalizamos mais umaa !!

Resposta

1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios 11 a 19, calcular o volume do sólido delimitado pelas superfícies dadas.11. x 2 + y 2 = 16 ; z = 2 e x + z = 9 .
Calcular o volume do sólido delimitado por z = 8 - x 2 - 2 y 2 , no primeiro octante.
Calcular o volume da parte da esfera x 2 + y 2 + z 2 = 9 entre os planos z = 1 e z = 2 .
Nos exercícios 11 a 19, calcular o volume do sólido delimitado pelas superfícies dadas.12. x 2 + 2 y 2 = 2 ; z = 0 e z = x + 4 .
Calcular o volume do tetraedro da Figura 8.32.Entre os planos z = 1 e z = 2 ;Acima do plano z = 1 ; Abaixo do plano z = 2 .