Integrais Triplas

Fala galera bonita. Sejam muito bem vindos ao Responde Aí. Nós somos a plataforma de exatas que vai salvar o seu semestre!

Nossa missão aqui hoje é dar uma introdução sobre as integrais triplas. Vamos lá?

Conhecimentos Prévios

✅ Integrais

✅ Integrais Duplas

Integrais Triplas

Quando a gente começa a estudar as integrais triplas, normalmente, a gente já passou pelas integrais simples e pelas integrais duplas. E a gente achava que não dava para piorar, né? hahaha. Brincadeirinha, não é tão complicado quanto parece.

Enquanto as integrais simples o intervalo de integração era (um comprimento) e para as duplas era (uma área), para as triplas teremos um volume infinitesimal , que pode ser representado assim:

Sendo assim, se queremos fazer a integral de uma função sob um volume, , como esse que mostra a imagem acima, temos que fazer o seguinte:

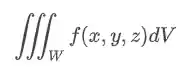
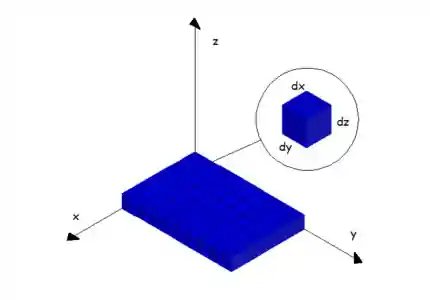
Vamos supor que no nosso volume, , pertence ao intervalo , ao intervalo e ao intervalo . Assim para resolver a integral tripla temos que fazer a integração em relação a cada uma das variáveis uma de cada vez, desse jeito aqui:

Topa fazer um exemplo rapidinho para entender melhor como funciona?

Exemplo

Calcule a seguinte integral:

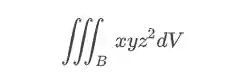
Onde é o paralelepídedo dado por:

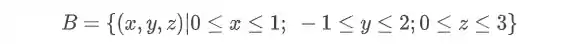
Vamos fazer a resolução passo a passo, beleza?

Passo 1

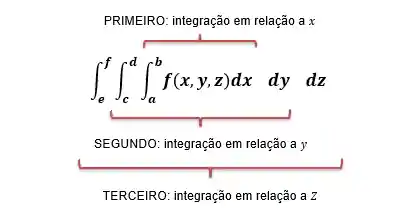
O primeiro passo é montar a integral tripla substituindo os intervalos de integração e estabelecendo a ordem de cálculo.

Vamos usar como ordem de cálculo , então temos que colocar o intevalo de na integral mais interna, o intervalo de na do meio e o intervalo de na mais externa, desse jeito aqui:

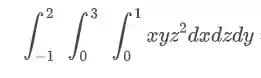
Passo 2

O póximo passo é realizar a integração em relação a :

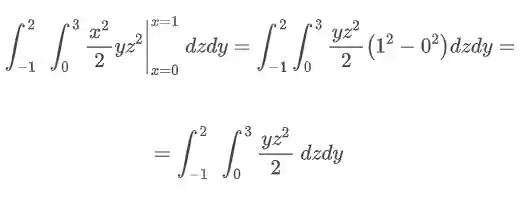
Passo 3

E o terceiro e último passo é integrar em relação a seguido da integração em relação a :

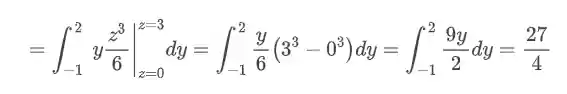
E temos o resultado!

Tranquilo não é?

Isso é apenas uma introdução sobre as integrais triplas. E se você quiser pode ver essa introdução assistindo o vídeo aqui embaixo 👇🏽. Porque no Responde Aí tem conteúdo em texto e em vídeo também, você escolhe o que você preferir 😉

Mas, note que nessa introdução que vimos hoje o intervalo de integração eram números mesmo, mas e se a gente quiser calcular a integral limitando o , e a uma função, ou seja, o intervalo de integração vai ser uma função e não um número? 😱

Quer descobrir como calcular a integral tripla nesse caso e muito mais coisas? Então confere o nosso Raio-X aqui embaixo 👇🏽, onde nós organizamos todo o conteúdo que você precisa saber sobre as integrais triplas em capítulos e tópicos para o seu estudo ser focado, rápido e lógico.

Está esperando o que para decidir de vez estudar com Responde Aí?