7) Calcule
onde γ é uma curva
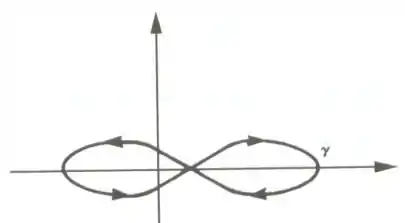
Passo 1
Olá, tudo bem?
Agora é hora de você aprender um pouco mais sobre cálculo. Mais especificamente você irá aprender sobre o teorema de Green.
O teorema de Green diz que
Definimos nessa questão o campo vetorial como:
Passo 2
Um campo é conservativo se:
Vamos calcular então:
Usando a regra do quociente para realizarmos essas derivadas parciais:
Portanto:
Nesse caso o nosso campo é conservativo, mas com um problema, não é definido em
Passo 3
O campo não é conservativo em todo o domínio, porque ele não é definido na origem , que está dentro da região limitada por .
Logo, não podemos aplicar o Teorema de Green diretamente
Para aplicar o Teorema de Green com um buraco no meio, podemos dividir a curva em duas laçadas (laço da esquerda e laço da direita), cada uma percorrida no sentido anti-horário.
Parametrizando uma curva que envolve a origem uma vez no sentido anti-horário:
Substituindo na integral: