Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 9.3 - Ex. 10

10 . Calcule a área de z = sqrt(x^2 + y^2) , x^2 + y^2 <= 2 x , x >= 1 e y >= 0

Passo 1

Pode até parecer confuso quando temos 2 equações, fica aquela dúvida de “qual superfície usar?”. Bem vamos traduzir o que esse exercício diz, temos então uma casca cônica limitada por uma região.

E essa região limitada da casca cônica que vamos calcular

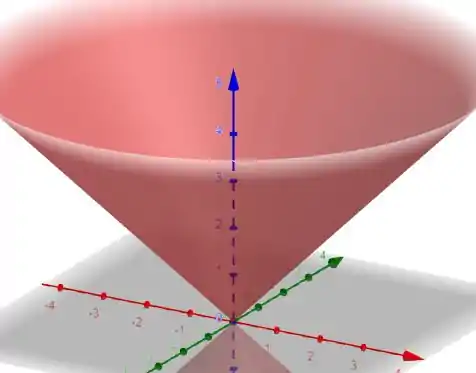
. Lembrando que nossa estrutura de cálculo é

int int_S^() d S = int int_(R ')^() sqrt(1 + ((del z)/(del y))^2 + ((del z)/(del x))^2) d y d x

Passo 2

Então vamos usar nossa equação do cone e projetar ela no plano XY

x^2 + y^2 = z^2

Logo como vamos projetar em XY, vamos isolar z

z = sqrt(x^2 + y^2 )

Só nos resta agora calcular as derivadas parciais de z

z_x = (x)/(sqrt(x^2 + y^2))

z_y = (y)/(sqrt(x^2 + y^2))

Passo 3

Vamos Unir o que já calculamos a nossa integral

int int_(R ')^() sqrt(1 + ((del z)/(del y))^2 + ((del z)/(del x))^2) d y d x

int int_(R ')^() sqrt(1 + ((y)/(sqrt(x^2 + y^2)))^2 + ((x)/(sqrt(x^2 + y^2)))^2) d y d x

int int_(R ')^() sqrt(1 + (x^2 + y^2)/(x^2 + y^2)) d y d x

int int_(R ')^() sqrt(2) d y d x

= sqrt(2) int int_(R ')^() d y d x

Beleza agora só precisamos encontrar o intervalo de integração e isso é dado pela nossa região que limita o cone

x^2 + y^2 <= 2 x

x >= 1

y >= 0

Isso quer dizer que queremos calcular área da interseção dessas 3 regioes

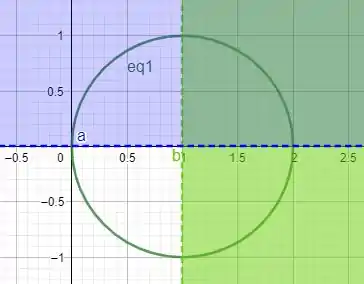
Ou seja queremos o primeiro quadrante de um circulo unitário. E como nossa integração apenas quer uma área ( como podemos perceber pela equação )

sqrt(2) int int_(R ')^() d y d x

Então podemos encurtar os cálculos e calcular a área com as formulas de Em. médio

A_c i r c u l o = (1)/(4) (pi * 1 ²)

A = (pi)/(4)

Logo a área da nossa superfície é

sqrt(2) int int_(R ')^() d y d x -> sqrt(2) * (pi)/(4)

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

int int_(R ')^() sqrt(1 + ((del z)/(del y))^2 + ((del z)/(del x))^2) d y d x = sqrt(2) * (pi)/(4)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a massa da superfície σ dada, com função densidade superficial de massa f ( x , y , z ) dada: f x , y , z = z e σ é a superfície x 2 + y 2 + z 2 = 1 ,z ≥ 0 .
Calcule a massa da superfície σ dada, com função densidade superficial de massa f ( x , y , z ) dada: b )f x , y , z = x 2 + y 2 + z 2 e σ é a superfície z 2 = x 2 + y 2 ,1 ≤ z ≤ 2 .
Seja f : a , b → R uma função de classe C 1 , com f u ≥ 0 em a , b . Considere a superfície de revolução σ u , v = f u cos ⁡ v , f u s e nv ,u , com a ≤ u ≤ b ,0 ≤ v ≤ 2 π . Estabeleça uma fórmula par
Seja σ u , v = x u , v , y u , v , z u , v , u , v ∈ K . Mostre que a área de σ pode ser expressa na forma á r e ad eσ = ∬ K ∂ y , z ∂ u , v 2 + ∂ z , x ∂ u , v 2 + ∂ x , y ∂ u , v 2 d u d vá Sugestão
Estabeleça uma fórmula para o cálculo da área da superfície x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 , onde a0 ,bb ,c0 são constantes dadas