Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 16.2 - Ex. 8

Calcule a integral de linha, onde C é a curva dada.

∫ C x y   d x + 2 y x   d y ,

C consiste na metade superior da circunferência x 2 + y 2 = 1 de ( 1 ,   0 ) a ( 1 ,   0 ) e no segmento de reta de ( 1 ,   0 ) até ( 4 ,   3 ) .

Passo 1

Antes de começar a resolver o problema, note que a curva C não faz muito sentido pelo que foi dado no enunciado: ele diz que se trata da metade superior da circunferência porém do ponto ( 1 ,   0 ) até ele mesmo, o que é estranho...

Outra coisa estranha que aparece é que tanto x como y estão dentro de uma raiz quadrada, de modo que eles devem ser positivos... Por isso, devemos restringir nosso problema ao primeiro quadrante!

Sendo assim, prefiro refazer o enunciado da seguinte forma:

“ C consiste na metade superior da circunferência x 2 + y 2 = 1 de ( 1 ,   0 ) a ( 0 ,   1 ) e no segmento de reta de ( 0 ,   1 ) até ( 4 ,   3 ) .”

Vou resolver a questão com esse enunciado! Fazendo um esboço da região de integração, obtemos:

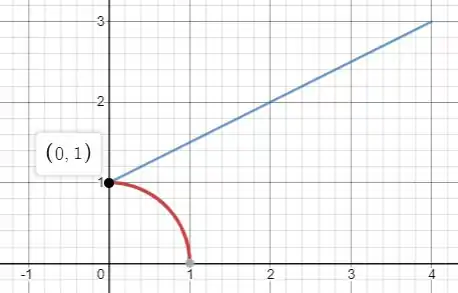
Assim, temos que fazer a integral sobre duas curvas: o trecho da circunferência em vermelho e a reta em azul.

Passo 2

Para o trecho em vermelho, vamos usar a parametrização

x t = cos ⁡ t             e             y t = s e n   t

Assim,

d x = - s e n   t   d t             e             d y = cos ⁡ t   d t

Desta forma, a integral sobre essa curva será

I = ∫ 0 π / 2 cos ⁡ t s e n   t   - s e n   t   d t + 2   s e n   t   cos ⁡ t cos ⁡ t   d t

Essa integral pode ser quebrada em duas partes:

I = I 1 + I 2 ,

onde

I 1 = - ∫ 0 π / 2 s e n   t   s e n   t cos ⁡ t   d t

I 2 = 2 ∫ 0 π / 2 cos ⁡ t cos ⁡ t   s e n   t   d t

Para a primeiro integral, fazemo u = s e n   t , de modo que d u = cos ⁡ t   d t :

I 1 = - ∫ s e n   0 s e n   π u u   d u = - ∫ 0 1 u 3 2   d u = - 2 5 u 5 2 0 1 = - 2 5

Já para I 2 , fazemos u = cos ⁡ t , de modo que d u = - s e n   t   d t :

I 2 = - 2 ∫ 1 0 u u   d u = 2 ∫ 0 1 u 3 2   d u = 4 5

Assim,

I = - 2 5 + 4 5 = 2 5

Passo 3

Já para o trecho em azul, podemos fazer a parametrização da seguinte forma:

x t = t               e             y t = 1 + t 2

Essa parametrização refleta à reta y = 1 + x 2 . Neste caso, temos que 0 ≤ t ≤ 4 . Assim,

d x = d t           e           d y = d t 2

Portanto, a integral de linha sobre essa curva será

J = ∫ 0 4 t 1 + t 2   d t + 2 1 + t 2 t d t 2

Logo,

J = ∫ 0 4 t 1 + t 2   d t + ∫ 0 4 t + t t 2   d t

Para a primeira integral, fazemos

u = 1 + t 2 ⇒ d u = d t 2 ⇒ d t = 2   d u

Assim,

J 1 = ∫ 0 4 t 1 + t 2   d t = ∫ 1 3 2 u - 1 u ⋅ 2   d u = 4 ∫ 1 3 u 3 2 - u 1 2   d u

Portanto,

J 1 = 4   2 5 u 5 2 - 2 3 u 3 2 1 3 = 4 2 5 ⋅ 9 3 - 2 3 ⋅ 3 3 - 2 5 + 2 3 = 4 4 15 + 8 3 5

Já para a segunda integral, temos que

J 2 = ∫ 0 4 t 1 2 + 1 2 t 3 2   d t = 2 3 t 3 2 + 1 5 t 5 2 0 4 = 2 3 ⋅ 8 + 1 5 ⋅ 32 = 176 15

Portanto,

J = 16 15 + 32 3 5 + 176 15 = 192 15 + 32 3 5

Logo,

J = 64 5 + 32 3 5

Passo 4

A integral sobre C é dada por

∫ C x y   d x + 2 y x   d y = I + J = 2 5 + 64 5 + 32 3 5

Portanto,

∫ C x y   d x + 2 y x   d y = 66 5 + 32 3 5

Resposta

66 5 + 32 3 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja F → um campo vetorial contínuo em R 2 . Justifique as igualdades. ∫ γ 1 F → ⋅ d γ → 1 = ∫ γ 2 F → ⋅ d γ → 2 Onde γ 1 t = cos ⁡ t , s e nt , 0 ≤ t ≤ 2 π , e γ 2 u = cos ⁡ 2 u , s e n2 u ,0 ≤ u ≤ π
Seja F → um campo vetorial contínuo em Ω e sejam γ 1 : a , b → Ω e γ 2 : c , d → Ω duas curvas quaisquer de classe C 1 , tais que I mγ 1 = I mγ 2 . A afirmação ∫ γ 1 F → ⋅ d γ 1 = ∫ γ 2 F → ⋅ d γ 2 Ou
Calcule ∫ γ d x + d y , onde γ é o poligonal de vértice A 0 = 0,0 , A 1 = 1,2 , A 2 = - 1,3 , A 3 = - 2,1 e A 4 = - 1 , - 1 , sendo γ orientada de A 0 para A 4 .
Calcule int_gamma x^2 d x + y^2 d y + z^2 d z onde gamma é a curva do Exercício 5.
Calcule ∫ γ x - y d x + e x + y d y , onde γ é a fronteira do trinângulo de vértice 0,0 ,0,1 e 1,2 , orientada no sentido antí-horário.