Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.7 - Ex. 31

Calcule a integral de superfície ∫ ∫ S   F ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação positiva (para fora).

F x ,   y ,   z = x 2   i + y 2   j + z 2   k  

S é a fronteira do semicilindro sólido 0 ≤ z ≤ 1 - y 2   ,     0 ≤ x ≤ 2   .

Passo 1

Faaaala minha turma, beleza!?

Precisamos calcular o fluxo de F através de S .

F x ,   y ,   z = x 2   i + y 2   j + z 2   k  

Onde,

S é a fronteira do semicilindro sólido 0 ≤ z ≤ 1 - y 2   ,     0 ≤ x ≤ 2   .

Primeiro vamos analisar um esboço do semicilindro:

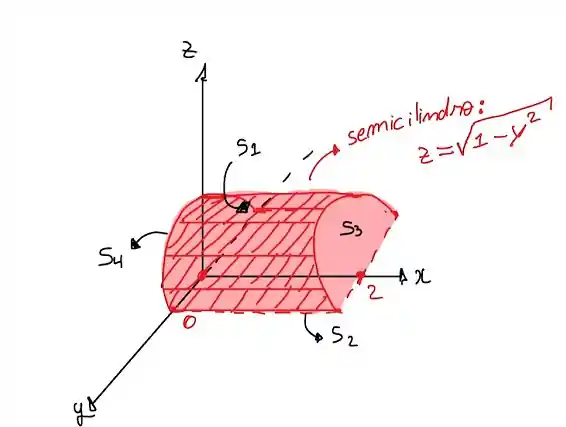
Aqui S consiste de quatro superfícies:

S 1 , o topo da superfície (uma porção do cilindro y 2 + z 2 = 1 );

S 2 , a parte inferior (uma porção do plano x y );

S 3 , a metade do disco no plano x = 2 ;

S 4 , a metade do disco no plano x = 0 .

Vamos ter que calcular o fluxo em cada superfície, e no final somar tudo. Desse jeito:

∫ ∫ S   F ∙ d S = ∫ ∫ S 1   F ∙ d S + ∫ ∫ S 2   F ∙ d S + ∫ ∫ S 3   F ∙ d S + ∫ ∫ S 4   F ∙ d S

Onde, d S = n d A

Então vamos usar uma das seguintes formulas como estratégia:

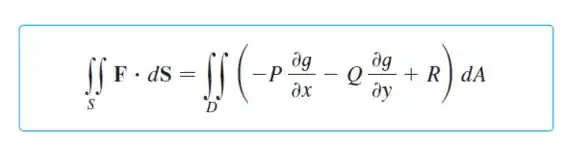
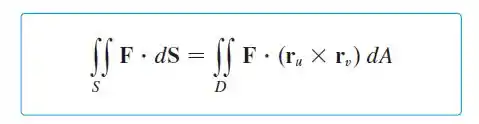
Onde P , Q e R são as componentes de F :

F x ,   y ,   z = P   i + Q   j + R   k  

E, g ( x , y ) = z . Repare que aparece as derivadas de g em relação a x e y .

E, ( r u   ×   r v ) é o produto vetorial das derivadas da parametrização r em relação a u e v .

Feito isso, substituímos na integral e resolvemos.

Vamos lá então, gabaritar essa juntos!

Passo 2

Vamos começar pela superfície S 1 , o topo da superfície.

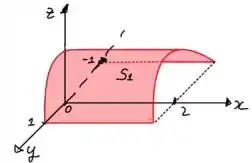
A superfície é z = 1 - y 2 para 0 ≤ x ≤ 2   ,     - 1 ≤ y ≤ 1   , com orientação para cima.

Sabemos que F é:

F x ,   y ,   z = x 2   i + y 2   j + z 2   k  

Repare que temos:

g x , y = z = 1 - y 2

Logo, a integral fica:

∫ ∫ S 1   F ∙ d S = ∫ ∫ S 1   - P ∂ g ∂ x - Q ∂ g ∂ y + R d y   d x

∫ ∫ S 1   F ∙ d S = ∫ 0 2 ∫ - 1 1 - x 2 0 - y 2 - y 1 - y 2 + z 2 d y   d x

Ou seja, vamos ter que substituir z na integral para ficar somente em função de x e y . Desse jeito:

∫ 0 2 ∫ - 1 1 y 3 1 - y 2 + 1 - y 2 d y   d x

Agora vamos começar a integrar, lembrando que começamos de dentro para fora.

Integrando em d y , temos:

∫ 0 2 - 1 - y 2 + 1 - y 2 3 2 3 + y - y 3 3 y = - 1 y = 1 d x

Aplicando os limites de integração, temos:

∫ 0 2 - 1 - 1 2 + 1 - 1 2 3 2 3 + 1 - 1 3 3 - - 1 - - 1 2 + 1 - - 1 2 3 2 3 - 1 - ( - 1 ) 3 3 d x

Agora é só ir simplificando, somando e subtraindo os termos. Desse jeito:

∫ 0 2 - 0 + 0 + 1 - 1 3 - - 0 + 0 - 1 + 1 3 d x

Assim, ficamos com a seguinte integral:

∫ 0 2 4 3   d x

Integrando em d x vamos ter:

4 3 x 0 2

Aplicando os limites de integração, vamos ter que o fluxo através de S 1 é:

∫ ∫ S 1   F ∙ d S = 8 3

Passo 3

Agora vamos resolver para a superfície em S 2 .

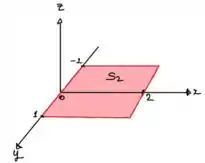
A superfície é z = 0 com orientação para baixo, ou seja,

g x , y = z = 0

Substituindo na integral, vamos ter:

∫ ∫ S 2   F ∙ d S = ∫ ∫ S 2   - P ∂ g ∂ x - Q ∂ g ∂ y + R d y   d x

Sabemos que F é:

F x ,   y ,   z = x 2   i + y 2   j + z 2   k  

Logo:

∫ ∫ S 2   F ∙ d S = ∫ 0 2 ∫ - 1 1 - z 2 d y   d x

Como z = 0 , temos:

∫ 0 2 ∫ - 1 1 ( 0 ) d y   d x

Desse jeito, o fluxo através da superfície S 2 é igual a:

∫ ∫ S 2   F ∙ d S = 0

Passo 4

Em S 3 , a superfície é x = 2 para - 1 ≤ y ≤ 1   ,     0 ≤ z ≤ 1 - y 2   , orientada para o sentido positivo do eixo x .

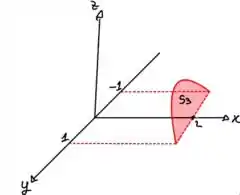
Como z está variando, vamos ter que usar a seguinte integral:

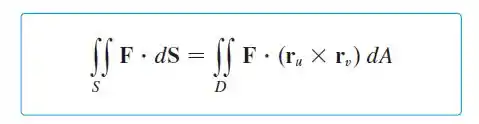
Podemos então escrever a seguinte parametrização para a curva:

r y ,   z = 2   i + y   j + z   k   ,             - 1 ≤ y ≤ 1   ,           0 ≤ z ≤ 1 - y 2

Sabemos que F é:

F x ,   y ,   z = x 2   i + y 2   j + z 2   k  

Logo:

F r y ,   z = 4   i + y 2   j + z 2   k

Para o produto vetorial ( r y × r z ) , vamos ter que achar as derivadas antes:

r y = d r d y = 0 i + 1 j + 0 k

r z = d r d z = 0 i + 0 j + 1 k

Assim, vamos ter que o produto vetorial é:

( r y × r z ) = i j k 0 1 0 0 0 1

Aplicando o determinante, vamos ter que o produto vetorial é:

r y × r z = i + 0   j + 0   k

Portanto, substituindo na integral temos:

∫ ∫ S 3   F ∙ d S = ∫ - 1 1 ∫ 0 1 - y 2 4 , y 2 , z 2 ∙ 1,0 , 0 d z   d y

Fazendo o produto escalar, vamos ter:

∫ - 1 1 ∫ 0 1 - y 2 4 d z   d y

Agora eu quero que você preste bem atenção! Observe que temos uma integral, que vai dar 4 vezes a área de S 3 :

∫ ∫ S 3   F ∙ d S = 4 ∫ - 1 1 ∫ 0 1 - y 2 d z   d y

O grande truque, é que conhecemos uma formula para a área da região S 3 . Ela é metade de uma circunferência, certo! Logo, a fórmula da área é:

A S 3 = 1 2 π r 2

Podemos substituir essa fórmula direto na integral. Desse jeito:

4 ∫ - 1 1 ∫ 0 1 - y 2 d z   d y = 4 A S 3

Como o raio desse círculo é 1 temos:

4 A S 3 = 4 1 2 π 1 2 = 2 π

Logo, temos que o fluxo através da superfície S 3 é:

∫ ∫ S 3   F ∙ d S = 2 π

Passo 5

Por último, em S 4 , a superfície é x = 0 para - 1 ≤ y ≤ 1   ,     0 ≤ z ≤ 1 - y 2   , mas orientada para o sentido negativo do eixo x .

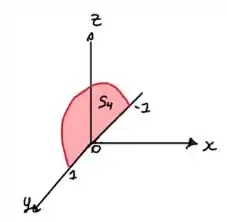
Podemos então escrever a seguinte parametrização para essa curva:

r y ,   z = 0   i + y   j + z   k   ,             - 1 ≤ y ≤ 1   ,           0 ≤ z ≤ 1 - y 2

Novamente, vamos usar a seguinte integral:

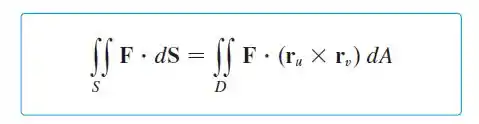
Sabemos que F é:

F x ,   y ,   z = x 2   i + y 2   j + z 2   k  

Logo:

F r y ,   z = 0   i + y 2   j + z 2   k

Para o produto vetorial ( r y × r z ) , vamos ter que achar as derivadas antes:

r y = d r d y = 0 i + 1 j + 0 k

r z = d r d z = 0 i + 0 j + 1 k

Assim, vamos ter que o produto vetorial é:

( r y × r z ) = i j k 0 1 0 0 0 1

Aplicando o determinante, vamos ter que o produto vetorial é:

r y × r z = i + 0   j + 0   k

Portanto, substituindo na integral temos:

∫ ∫ S 4   F ∙ d S = ∫ - 1 1 ∫ 0 1 - y 2 0 , y 2 , z 2 ∙ 1,0 , 0 d z   d y

Portanto, resolvendo o produto escalar vamos ter:

∫ ∫ S 4   F ∙ d S = ∫ - 1 1 ∫ 0 1 - y 2 0   d z   d y

Logo, concluímos que o fluxo através da superfície S 4 é:

∫ ∫ S 4   F ∙ d S = 0

Finalmente, podemos somar tudo:

∫ ∫ S   F ∙ d S = ∫ ∫ S 1   F ∙ d S + ∫ ∫ S 2   F ∙ d S + ∫ ∫ S 3   F ∙ d S + ∫ ∫ S 4   F ∙ d S

∫ ∫ S   F ∙ d S = 8 3 + 0 + 2 π + 0

Logo, o fluxo através da superfície S vai ser:

∫ ∫ S   F ∙ d S = 2 π + 8 3

Resposta

∫ ∫ S   F ∙ d S = 2 π + 8 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja T a superfície do tetraedro limitado pelos planos coordenados e o plano x + y + z = 4 . Calcular I =∫ ∫ S y z d y d z + x z d z d x + x y d x d y = OndeS é a face da frente de TS é a face de T qu
Calcular ∫ ∫ S f → *n →d S Sendo f → = xi → + yj → +z k → e S a parte do plano 2 x + 3 y + 4 z = 12 cortada pelos planos x= 0 ,y = 0 ,x = 1 ,y = 2 e n → é a normal com componente z não negativa
Um fluido tem um vetor densidade de fluxo f → = x i → - 2 x + y j → + k .→ Sejam S hemisfério x ² + y ² + z ² = 4 ² ² ² , z ≥ 0 e n → a normal que aponta para fora . Calcular a massa de fluido que atr
Seja T a superfície do tetraedro limitado pelos planos coordenados e o plano x + y + z = 4 . Calcular I =∫ ∫ S y z d y d z + x z d z d x + x y d x d y = OndeS é a face da frente de TS é a face de T qu
Seja T a superfície do tetraedro limitado pelos planos coordenados e o plano x + y + z = 4 . Calcular I =∫ ∫ S y z d y d z + x z d z d x + x y d x d y = OndeS é a face da frente de TS é a face de T qu