Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios de Caso Vetorial - Lista de Exercícios Resolvida

Ver Teoria

Questão 1

Calcule a integral:

∬ S F ∙ n d S

Onde:

F = - 3 x y z 2 , x + 2 y z - 2 x z 4 , y z 3 - z 2

E S é a união da superfície: x 2 + y 2 = 1

0 ≤ z ≤ 1

Com a superfície:

z = 0

x 2 + y 2 ≤ 1

Indicando a orientação escolhida para S .

Ver solução completa

Questão 2

Calcule

∬ S   x z   d y ∧ d z + z y 2 d z ∧ d x + y 2 2 d x ∧ d y

Onde

S = x , y , z ∈ R 3 x 2 + y 2 + z 2 = 4 ,   x 2 + y 2 ≤ 2 x ,   z ≥ 0

Orientada pela normal N → com N → . k → > 0 .

Ver solução completa

Questão 3

Encontre o fluxo do campo vetorial F através de σ . Onde F x ,   y ,   z = x + y i + y + z j + z + x k ; σ é a porção do plano x + y + z = 1 do primeiro octante, orientada por vetores normais unitários com componentes positivos.

Ver solução completa

Questão 4

Calcule ∬ S   F → . N → d σ , sendo F → x , y , z = - y i → + x j → + z k → e S a parte de x 2 + y 2 + z 2 = 1 que satisfaz 2 2 ≤ z ≤ 3 2 , orientada pela normal N → tal que N → . k → > 0 .

Ver solução completa

Questão 5

Seja S a superfície de revolução obtida girando a curva C , definida pela equação

y = e x ,             x ∈ [ 0,1 ]

Em torno do eixo O X com vetor normal apontando para o lado do eixo de revolução. Calcule o fluxo do campo vetorial

F → x , y , z = x z 2 + y 2 , y , z

Através da superfície de revolução S .

Ver solução completa

Questão 6

Calcule ∬ S   F → . N → d S onde F → x , y , z = r → r → 3 → e S é a parte do hiperboloide x 2 + y 2 - z 2 = 1 limitado pela esfera x 2 + y 2 + z 2 = 2 com a normal que aponta no sentido que se afasta do eixo z .

Ver solução completa

Questão 7

Calcule

∬ S   x z   d y ∧ d z + z y 2 d z ∧ d x + y 2 2 d x ∧ d y

Onde

S = { x , y , z ∈ R 3 | x 2 + y 2 + z 2 = 4 ,   x 2 + y 2 ≤ 2 x ,   z ≥ 0

Orientada pela normal N → com N → . k → > 0 .

Ver solução completa

Questão 8

Calcule ∬ S   F → . N → d S onde F → x , y , z = x y , x 2 , ln ⁡ ( x 2 + y 2 ) e S é a parte da superfície z + 1 2 = x 2 + y 2 para 0 ≤ z ≤ 3 orientada de modo que N → é tal que N → . k → < 0 .

Ver solução completa

Questão 9

Calcule ∬ S   F → . N → d S sendo F → x , y , z = x 3 12 , y 3 48 , z e S é parte da superfície x 2 4 + y 2 16 = 1 , limitada pelos planos z = 3 e z = - 3 , orientada pela normal N → que se afasta do eixo z (exterior).

Ver solução completa

Questão 10

Calcule:

∬ S   F ∙ n d S

Onde F x , y , z = ( 2 y , - z , x 2 ) e S é a superfície do cilindro y 2 = 8 x situada no primeiro octante e limitada pelos planos y = 4 e z = 6 . Oriente a normal de forma que sua coordenada x seja positiva.

Ver solução completa

Questão 11

Seja S parte do plano x + 3 y + 2 z = 8 limitada pelos planos x = 0 , y = 0 e z = 0 . Calcule

∬ S F → ∙ N → d S

Onde F → x , y , z = ( x y z , y 2 z , x y ) com N → ∙ k → > 0

Ver solução completa

Questão 12

(Capítulo 16.7 – Exercício 21) Avalie a integral de superfície ∬ S F → ⋅ d S → para o campo vetorial dado F → e a superfície orientada S . Em outras palavras, localize o fluxo de F → através de S . Para superfícies fechadas, use a orientação (para o exterior) positiva.

F x , y , z = z e x y i ^ - 3 z e x y j ^ + x y k ^

S é o paralelogramo do Exercício 5 com orientação ascendente.

Ver solução completa

Questão 13

23) Calcule

∬ S   F → ⋅ n →   d S

a) F → x ,   y ,   z = - z k → e S é a parte da esfera x 2 + y 2 + z 2 = 4 fora do cilindro x 2 + y 2 = 1 , n → apontando para fora.

Ver solução completa

Questão 14

23) Calcule

∬ S   F → ⋅ n →   d S

h) F → x ,   y ,   z = z i → + y z j → e S é a parte do plano z = 2 - x , limitada pelo cilindro x 2 + y 2 = 9 , com n → tal que n → ⋅ k → ≥ 0 .

Ver solução completa

Questão 15

23) Calcule

∬ S   F → ⋅ n →   d S

d) F → x ,   y ,   z = - 3 x y z 2 i → + x + 2 y z - 2 x z 4 j → + y z 3 - z 2 k → e S é a união da superfície

x 2 + y 2 = 1 , 0 ≤ z ≤ 1 , com z = 0 , x 2 + y 2 ≤ 1 , indicando a orientação escolhida para S .

Ver solução completa

Questão 16

23) Calcule

∬ S   F → ⋅ n →   d S

f) F → x ,   y ,   z = x ,   y ,   - z e S é a semiesfera x 2 + y 2 + z 2 = 4 , z ≥ 0 , com n → exterior.

Ver solução completa

Questão 17

Calcule o fluxo de F → x , y , z = x i → + y j → - 2 z k → , através da superfície S , parte do cilindro x 2 + y 2 = 2 x , limitado pelo plano z = 0 e pelo cone z = x 2 + y 2 , com vetor normal apontando para fora de S .

Ver solução completa

Questão 18

23) Calcule

∬ S   F → ⋅ n →   d S

l) F → x ,   y ,   z = x ,   - 3 y ,   - 2 z e S é a união dos planos y + z = 0 , com 0 ≤ x ≤ 1 , - 1 ≤ y ≤ 0 e z = 0 , com 0 ≤ x ≤ 1 , 0 ≤ y ≤ 1 , indicando a orientação escolhida para S .

Ver solução completa

Questão 19

Seja S a parte de o cilindro x 2 + y 2 = 4 limitada pelos planos z = - 1 e z = 1 e orientada pela normal unitária N → , tal que N → 1,0 , 0 = i → e F → x , y , z = x   i → + y   j → + z 4   k → . O valor da integral

∫ ∫ S F → ⋅ N → d σ

é:

a) 4 π

b) 20 π

c) 8 π

d)   12 π

e) 16 π

Ver solução completa

Questão 20

Calcule o fluxo de F → x , y , z = y 2 + z 2 , x , x , através da superfície de revolução obtida girando o segmento de reta que liga o ponto 4,1 , 0 a 2,4 , 0 em torno do eixo x , onde o vetor n → tem componente i → não negativa.

Ver solução completa

Questão 21

Calcule ∬ S F → . n → d S , onde

F → x , y , z = x 2 + y 2 + z 2 - 3 2 x , y , z e S é a esfera x 2 + y 2 + z 2 = a 2 ,   a > 0 , com n → exterior.

Ver solução completa

Questão 22

Calcule ∬ S   F → . N → d σ , sendo F → x , y , z = - y i → + x j → + z k → e S a parte de x 2 + y 2 + z 2 = 1 que satisfaz 2 2 ≤ z ≤ 3 2 , orientada pela normal N → tal que N → . k → > 0 .

Ver solução completa

Questão 23

Calcule ∬ S   F → . N → d S onde F → x , y , z = r → r → 3 → e S é a parte do hiperboloide x 2 + y 2 - z 2 = 1 limitado pela esfera x 2 + y 2 + z 2 = 2 com a normal que aponta no sentido que se afasta do eixo z .

Ver solução completa

Questão 24

Questão 1:

b) Calcule

∬ S   x   d y ∧ d z + y   d z ∧ d x + z   d x   ∧ d y

Sendo S a parte do plano z + 2 x - 3 = 0 limitada pelo paraboloide z = 4 - x 2 - 2 y 2 , orientada com a normal unitária de modo que N → ⋅ k → > 0 .

Ver solução completa

Questão 25

Seja S a parte do hiperboloide x 2 + z 2 - y 2 = 9 com z ≥ 0 , limitada por x 2 + y 2 = 4 , orientada com N → tal que N → . k → > 0 .

  1. Dê uma parametrização de S e uma expressão para o campo de vetores normais N → .
  2. Calcule ∬ S   F → . N →   d S , onde F → x , y , z = ( z , 2 z , x 2 ) .

Ver solução completa

Questão 26

Questão 4) Dados o campo vetorial F → x ,   y ,   z = y i → + x j → + x z k → e a superfície S dada por

S = x ,   y ,   z : z = x + y + 2 ,   x 2 + y 2 4 ≤ 1

Calcule

∬ S   r o t   F → ⋅ n → d S ,

em que n → é o vetor unitário apontando para baixo.

Ver solução completa

Questão 27

Questão 2: Calcule

∬ S   F → ⋅ n → d S

Onde F → x ,   y ,   z = x ,   0 ,   z e S é a parte do paraboloide y = x 2 + z 2 + 1 limitado pelo cilindro x 2 + z 2 = 16 e orientado por n → tal que n → ⋅ j → > 0 .

Ver solução completa

Questão 28

Seja F → = e - x 2 + y , z x , e z + 1 e S a semiesfera x 2 + y 2 + z 2 = 1 , z ≥ 0 , com a normal tendo coordenada z positiva em 0,0 , 1 .   Escrever a integral de superfície (não precisa calcular ela) ∬ S F   → ∙ n → d S usando:

1. A parametrização x , y → x , y , 1 - x 2 - y 2 ,   x , y x 2 + y 2 ≤ 1 } ,  

2. A parametrização ϕ , θ → s e n ϕ cos ⁡ θ , s e n ϕ s e n θ , cos ⁡ ϕ ,   ϕ , θ   ∈ [ 0 , π / 2 ] × [ 0,2 π ] ,

3. Calculando primeiro F n = F → ∙ n →   e escrevendo a integral de função escalar ∬ S F n d S   com respeito a parametrização ϕ , θ do item 2 .

Ver solução completa

Questão 29

Seja F → x , y , z = ( cos 2 ⁡ z , cos 2 ⁡ y ,   s e n   z ) e S a parte da superfície x = sen ⁡ y + cos ⁡ z limitada por z = 0 , z = 2 y = - 1 e y = 1 , orientada por N → tal que N → . i → < 0 . Calcule

∬ S   F → . N → d σ

Ver solução completa

Questão 30

Seja S a superfície de revolução obtida girando a curva C , definida pela equação

y = e x ,             x ∈ [ 0,1 ]

Em torno do eixo O X com vetor normal apontando para o lado do eixo de revolução. Calcule o fluxo do campo vetorial

F → x , y , z = x z 2 + y 2 , y , z

Através da superfície de revolução S .

Ver solução completa

Questão 31

Seja S o gráfico de f ( x ,   y )   =   x 2   +   y 2 ,   x 2   +   y 2   ≤   1 e n a normal a s com componente z   ≤   0 . Seja   F ⃗ ( x ,   y ,   z )   =   x 2 y i ⃗   −   x y 2 j ⃗   +   k ⃗ . Calcule ∫ ∫ S   F ⃗   ∙   n ⃗ d S .

Ver solução completa

Questão 32

23) Calcule

∬ S   F → ⋅ n →   d S

k) F → x ,   y ,   z = x i → + - y j → e S é a parte da esfera x 2 + y 2 + z 2 = a 2 , a ≥ 0 , no primeiro octante e n → apontando para a origem.

Ver solução completa

Questão 33

2. Calcule a integral de superfície ∫ ∫ S F . d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação (para fora) positiva.

b) F x , y , z = x z e y i - x z e y j + z k , S é a parte do plano x + y + z = 1 no primeiro octante, com orientação para baixo.

Ver solução completa

Questão 34

2. Calcule a integral de superfície ∫ ∫ S F . d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação (para fora) positiva.

a) F x , y , z = x y i + y z j + z x k , S é a parte do paraboloide z = 4 - x 2 - y 2 que está acima do quadrado 0 ≤ x ≤ 1 , 0 ≤ y ≤ 1 , com orientação para cima.

Ver solução completa

Questão 35

Considere a superfície S do paraboloide z = 9 - x 2 - y 2 , situada no primeiro octante ( x ≥ 0 ,   y ≥ 0 ,   z ≥ 0 ) .

a) Ache uma parametrização para S .

c) Calcule o fluxo do campo F x , y , z = - y , x , - z através de S (supondo S orientada para fora).

Ver solução completa

Questão 36

(Capítulo 16.7 – Exercício 23) Avalie a integral de superfície ∬ S F → ⋅ d S → para o campo vetorial dado F → e a superfície orientada S . Em outras palavras, localize o fluxo de F através de   S . Para superfícies fechadas, use a orientação (para o exterior) positiva.

F → x , y , z = x y i ^ + y z j ^ + x z k ^

S é a parte do paraboloide z = 4 - x 2 y 2 que está acima do quadrado 0 ≤ x ≤ 1 ,   0 ≤ y ≤ 1 , e com orientação ascendente

Ver solução completa

Questão 37

(Cap.16.8- Exercício 2) Use o Teorema de Stokes para calcular ∬ S c u r l F → ⋅ d S → .

F → x , y , z = 2 y c o s z i → + e x s e n z j → + x e y k → , S é o hemisfério x 2 + y 2 + z 2 = 9 , z ≥ 0 , orientado para cima.

Ver solução completa

Questão 38

(Capítulo 16.7 – Exercício 31) Calcule a integral de superfície ∫ ∫ S   F ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação positiva (para fora).

F x ,   y ,   z = x 2   i + y 2   j + z 2   k   ,

S é a fronteira do semicilindro sólido 0 ≤ z ≤ 1 - y 2   ,     0 ≤ x ≤ 2   .

Ver solução completa

Questão 39

Questão 6. Calcule as seguintes integrais de superfícies.

(b) ∬ S y d S , S é a superfície z = 1 3 x 3 2 + y 3 2 , 0 ≤ x ≤ 1 , 0 ≤ y ≤ 1 .

Ver solução completa

Questão 40

Questão 6. Calcule as seguintes integrais de superfícies.

(c) ∬ S x 2 y 2 d S , S é a parte do cone z 2 = x 2 + y 2 que está entre os planos z = 1 e z = 3 .

Ver solução completa

Questão 41

(5) Seja a , b e c positivos. O fluxo do campo vetorial F → = 1 ,   b ,   c através da superfície do triângulo plano com vértices em 0 ,   0 ,   0 , a ,   0 ,   0 e 0 ,   b ,   c , orientada com normal cuja coordenada z é positiva, é igual a:

  1. 0
  2. 1
  3. - 1
  4. 2 a b c
  5. a b 2 c c 2 + b 2

Ver solução completa

Questão 42

Calcule a integral de superfície ∫ ∫ S F → ⋅ N → d σ   para cada um dos campos de vetores F → e superfícies orientadas S indicadas abaixo. Em outras palavras, calcule o fluxo de F → através de S . Quando S é uma superfície fechada, admita que S está orientada pela normal exterior.

a )   F → x , y , z = x 2 y i → - 3 x y 2 j → + 4 y 2 k → e S é a parte do parabolóide z = 9 - x 2 - y 2 , com z ≥ 0 , orientada de modo que a normal no ponto ( 0,0 , 9 ) é k → ;

Ver solução completa

Questão 43

Calcule a integral de superfície ∫ ∫ S F → ⋅ N → d σ   para cada um dos campos de vetores F → e superfícies orientadas S indicadas abaixo. Em outras palavras, calcule o fluxo de F → através de S . Quando S é uma superfície fechada, admita que S está orientada pela normal exterior.

b )   F → x , y , z = x i → + x y j → + x z k →   e S é a parte do plano 3 x + 2 y + z = 6 interior ao cilindro x 2 + y 2 = 1 , orientada de modo que seu vetor normal é 1 14 ( 3 i → + 2 j → + k → ) ;

Ver solução completa

Questão 44

Calcule a integral de superfície ∫ ∫ S F → ⋅ N → d σ   para cada um dos campos de vetores F → e superfícies orientadas S indicadas abaixo. Em outras palavras, calcule o fluxo de F → através de S . Quando S é uma superfície fechada, admita que S está orientada pela normal exterior.

c )   F → x , y , z =   - x i → - y j → + z 2 k → e S é a parte do cone z = x 2 + y 2 entre os planos z = 1 e z = 2 , orientada de modo que sua normal N → satisfaz N → ⋅ k → < 0 ;

Ver solução completa

Questão 45

Calcule a integral de superfície ∫ ∫ S F → ⋅ N → d σ   para cada um dos campos de vetores F → e superfícies orientadas S indicadas abaixo. Em outras palavras, calcule o fluxo de F → através de S . Quando S é uma superfície fechada, admita que S está orientada pela normal exterior.

d )   F → x , y , z = x i → + y j → + z k → e S é a esfera x 2 + y 2 + z 2 = 9 ;

Ver solução completa

Questão 46

Calcule a integral de superfície ∫ ∫ S F → ⋅ N → d σ   para cada um dos campos de vetores F → e superfícies orientadas S indicadas abaixo. Em outras palavras, calcule o fluxo de F → através de S . Quando S é uma superfície fechada, admita que S está orientada pela normal exterior.

e )   F → x , y , z =   - y i → + x j → + 3 z k → e S é o hemisfério z = 16 - x 2 - y 2 , orientada de modo que a normal no ponto ( 0,0 , 4 ) é k → ;

Ver solução completa

Questão 47

Calcule

a ∫ ∫ S x d y ∧ d z + y d z ∧ d x + z d x ∧ d y , onde S é a parte do plano   x   +   y   +   z   =   2 no primeiro octante, orientada de modo que sua normal satisfaz N . → j → > 0 ;

Ver solução completa

Questão 48

Seja C =   A B - ∪ B D - ∪ C 2 , sendo A = ( 1,0 ) , B = 1,2 ,   D = ( 0,2 ) e

C 2   : r t = π cos ⁡ t t , π sin ⁡ t t ,   t ∈ π 2 , 5 π 2

b) Esboce a curva C e o campo vetorial integrado no item a) em quatro pontos de C.

Ver solução completa

Questão 49

2. Calcule a integral de superfície ∫ ∫ S F . d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação (para fora) positiva.

a) F x , y , z = x y i + y z j + z x k , S é a parte do paraboloide z = 4 - x 2 - y 2 que está acima do quadrado 0 ≤ x ≤ 1 , 0 ≤ y ≤ 1 , com orientação para cima.

Ver solução completa

Questão 50

Considere a região elíptica R e o semi-elipsóide S do exercício 1. Considere também os campos

G → x , y , z = 1 2 - y i ^ + x j ^ e H → x , y , z = k ^

a) Assumindo que os vetores normais à R   e S tem componentes k ^ positivas, calcule

∫ ∫ R H → ⋅ n → d A e ∫ ∫ S H → ⋅ n → d A

b) Denote por C a elipse R   ∩   S . Orientando C de forma que o vetor tangente t em ( 1 ,   0 ,   0 ) tenha componente j ^ positiva, calcule

∫ C G ⋅ t d l

Ver solução completa

Questão 51

(Capítulo 16.7 – Exercício 25) Avalie a integral de superfície ∬ S F → ⋅ d S → para o campo vetorial dado F → e a superfície orientada S . Em outras palavras, localize o fluxo de F através de   S . Para superfícies fechadas, use a orientação (para o exterior) positiva.

F → x , y , z = x i ^ - z j ^ + y k ^

“ S   é a parte da esfera   x 2 + y 2 + z 2 = 4   no primeiro octante, com orientação para a origem.”

Ver solução completa

Questão 52

23) Calcule

∬ S   F → ⋅ n →   d S

c) F → x ,   y ,   z = z + 3 x i → + z + 3 k → e S é a superfície do sólido limitado por z = 1 - y 2 , x = 0 , x = 2 e o plano x y , com n → exterior.

Ver solução completa

Questão 53

Considere o campo vetorial

F x , y = x - 2 i + y   j + z k

Calcule a integral ∫ σ F ∙ n   d s onde o campo F é definido e σ é a superfície composta pelo cilindro x - 2 2 + y 2 = 4 , cortado por cima pelo plano z = 1 2 x + 4 + 6 , e completada por baixo pelo paraboloide z = x - 2 2 + y 2 , formando desta maneira um “copo”, com fundo parabólico e a parte lateral cilíndrica, deixando aberta a parte de cima. Sendo n apontando para fora do “copo”.

Ver solução completa

Questão 54

23) Calcule

∬ S   F → ⋅ n →   d S

g) F → x ,   y ,   z = y i → + x j → + 2 k → e S é a superfície plana limitada pelo triângulo de vértices 2 ,   0 ,   0 , 0 ,   2 ,   0 e 0 ,   0 ,   2 , com n → tendo a componente z não negativa.

Ver solução completa

Questão 55

Calcule a área lateral da superfície do solido dado por z ≤ 1 - y 2 ,   z ≤ 1 - x 2 e z ≥ 0 .

Ver solução completa

Questão 56

Seja S a superfície de um copo sem tampa, descrito a seguir: a lateral do copo é o cilindro x 2 + y 2 = 1 , - 4 ≤ z ≤ 0 ; o fundo do copo é a parte do plano z =   - 4 que se encontra dentro do cilindro. Considere o campo vetorial F x , y , z = f x , y , z x i + y j + z k , onde f ( x , y , z ) é uma função real (escalar) de classe C 1 em R 3 - { 0,0 , 0 } . Calcule ∬ r o t   F ∙ n d S onde n é a normal a S apontando para fora.

Ver solução completa

Questão 57

Calcule a integral de superfície ∫ ∫ S F → ⋅ N →   d σ para cada um dos campos de vetores F → e superfícies orientadas S indicadas abaixo. Em outras palavras, calcule o fluxo de F → através de S. Quando S é uma superfície fechada, admita que S está orientada pela normal exterior.

( f ) F → ( x , y , z ) = ( y ,   0 ,   - z ) e S consiste de parabolóide y = x 2   + z 2 , 0 ≤ y ≤ 1 e do disco x 2   + z 2 ≤ 1 , y = 1;

Ver solução completa

Questão 58

Calcule a integral de superfície ∫ ∫ S F → ⋅ N →   d σ para cada um dos campos de vetores F → e superfícies orientadas S indicadas abaixo. Em outras palavras, calcule o fluxo de F → através de S. Quando S é uma superfície fechada, admita que S está orientada pela normal exterior.

( g ) F → ( x , y , z ) = ( ( x + y ) , - ( 2 y + 1 ) ,     z ) e S é o retângulo de vértices (1, 0, 1), (1, 0, 0), ( 0, 1, 0), (0, 1, 1), orientado de modo que sua normal N → satisfaz N → . j ^ > 0 ;

Ver solução completa

Questão 59

Calcule a integral de superfície ∫ ∫ S F → ⋅ N →   d σ para cada um dos campos de vetores F → e superfícies orientadas S indicadas abaixo. Em outras palavras, calcule o fluxo de F → através de S. Quando S é uma superfície fechada, admita que S está orientada pela normal exterior.

( g ) F → ( x , y , z ) = ( x ,   2 y ,   3 z ) e S é o cubo de vértices (±1, ±1, ±1);

Ver solução completa

Questão 60

2. Calcule a integral de superfície ∫ ∫ S F . d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação (para fora) positiva.

c) F x , y , z = x i - z j + y k , S é a parte da esfera x 2 + y 2 + z 2 = 4 no primeiro octante com orientação para a origem.

Ver solução completa

Questão 61

3. Determine o fluxo de F ( x , y , z ) = s e n x y z i + x 2 y j + z 2 e x / 5 k através da parte do cilindro 4 y 2 + z 2 = 4 que está acima do plano x y e entre os planos x = - 2 e x = 2 com orientação para cima.

Ver solução completa

Questão 62

(Capítulo 16.7 – Exercício 30) Calcule a integral de superfície ∫ ∫ S   F ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação positiva (para fora).

F x ,   y ,   z = x   i + y   j + 5   k   ,

S é a fronteira da região delimitada pelo cilindro x 2 + z 2 = 1 e pelos planos y = 0 e x + y = 2 .

Ver solução completa

Questão 63

Dados o campo F → x , y , z = x z   i → + y z   j → - z 2 + z + e x 2 sen ⁡ y k → e a superfície fechada S que delimita o cilindro

E : x 2 + z 2 ≤ 9 ,   0 ≤ y ≤ 3

com a normal apontando para fora. Calcule:

(a) O fluxo de F → através da base de E que está contida no plano y = 0

Ver solução completa

Questão 64

  1. Explicite duas estratégias para calcular ∫ C F ∙ d r , onde F x , y =   < x 3 + x y 2 ,   y x 2 + y 3 + 3 x > e C a fronteira da região D = { x 2 9 + y 2 4 ≤ 1 }

Ver solução completa

Questão 65

23) Calcule

∬ S   F → ⋅ n →   d S

j) F → x ,   y ,   z = x - y ,   x + y ,   z e S : x 2 + y 2 = a 2 , z > 0 , 0 ≤ z ≤ h , com n → exterior.

Ver solução completa

Questão 66

23) Calcule

∬ S   F → ⋅ n →   d S

b) F → x ,   y ,   z = - x i → + - y j → + 3 y 2 z k → e S é a parte do cilindro x 2 + y 2 = 16 , situado no primeiro octante, entre z = 0 e z = 5 - y , n → apontando para o eixo z .

Ver solução completa

Questão 67

Sejam F → x , y , z = x 2 z ,   z e x 2 ,   x 2 + y 2 um campo vetorial e S a superfície dada por z = - 2 + x 2 + y 2 , com z ≤ 0 . Calcule

∬ F → ∙ n → d A

Sendo que n é o vetor normal de S que aponta para dentro.

Ver solução completa

Questão 68

Seja C o quadrado de vértices (5, 0), (0, 5), (−5, 0) e (0, −5), orientado no sentido anti-horário. Calcule

a integral de linha de campo vetorial

∫ ( y 2 x 2 - y x 2 + y 2 ) d x + ( x x 2 + y 2 + 2 x ) d y

Ver solução completa

Questão 69

23) Calcule

∬ S   F → ⋅ n →   d S

e) F → x ,   y ,   z = y z ,   - x z ,   x 2 + y 2 e S é a parte da superfície de revolução obtida girando o segmento de rata que liga 1 ,   0 ,   1   a 0 ,   0 ,   3 , em torno do eixo z , com n → tendo a componente z não negativa.

Ver solução completa

Questão 70

Calcule a integral de superfície ∬ S F → ∙ d S → , onde F → x ,   y ,   z = 1 x , 1 y , 1 z e S é a parte da esfera x 2 + y 2 + z 2 = a 2 , cujo contorno está definido como intercessão da esfera com dois planos horizontais paralelos e dois planos verticais concorrentes, que passam pelo eixo z , conforme à figura abaixo. A distância entre os planos horizontais é h , o ângulo entre os planos verticais é ω , S pertence ao primeiro octante, e o vetor normal aponta fora da esfera.

Ver solução completa

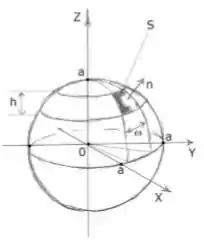
Questão 71

Calcule a integral de superfície.

∬ y d S

S é o helicoide com equação vetorial r u , v =   u c o s v i + u s e n v j + v k , 0 ≤ u ≤ 1 ,   0 ≤ v ≤ π

Ver solução completa

Questão 72

(ii) Escolha uma das estratégias para resolver ∫∫ FdS.

Ver solução completa

Questão 73

Calcule a integral de superfície ∫ ∫ S F → ⋅ N → d σ para cada um dos campos de vetores F → e superfícies orientadas S indicadas abaixo. Em outras palavras, calcule o fluxo de F → através de S . Quando S é uma superfície fechada, admita que S está orientada pela normal exterior.

( j ) F → ( x , y , z ) = y   i → + z   j → + x   k →   e S é a parte da superfície z = 4 - x limitada pela superfície cilíndrica y 2 = x , orientado de modo que a sua normal N → satisfaz N → ⋅ i → > 0 ;

Ver solução completa

Questão 74

Calcule a integral de superfície ∫ ∫ S F → ⋅ N → d σ para cada um dos campos de vetores F → e superfícies orientadas S indicadas abaixo. Em outras palavras, calcule o fluxo de F → através de S . Quando S é uma superfície fechada, admita que S está orientada pela normal exterior.

( i ) F → ( x , y , z ) = - y z   i →   e S é a parte da esfera x 2 + y 2 + z 2 = 4 exterior ao cilindro x 2 + y 2 ≤ 1 , orientada de modo que a normal no ponto ( 2,0 , 0 ) é i → ;

Ver solução completa

Questão 75

4. Considere um escoamento com velocidade v → x , y , z e densidade ρ x , y , z , tal que F → = ρ v → seja dado por F → = x i → + y j → - 2 z k → . Seja S a superfície x 2 + y 2 + z 2 = 4 , z ≥ 2 e seja n → a normal com componente z > 0 . Calcule o fluxo de F → através de S .

Ver solução completa

Questão 76

5 Considere, novamente, o campo F → = x i → + y j → - 2 z k → . Seja B a esfera x 2 + y 2 + z 2 ≤ 4 , calcule ∬   F → ∙ n → d S , em que S é a fronteira de B , com n → apontando para fora de B .

Ver solução completa

Questão 77

Seja F → ( x , y , z ) =   ( 𝑥   +   𝑦   +   𝑧 2   ) k → e seja S a fronteira do cilindro x 2 + y 2 ≤ 4 e 0   ≤   𝑧   ≤   3 . Calcule ∫ ∫ S F → ⋅ n →   d S , em que n → é a normal que aponta para fora do cilindro.

Ver solução completa

Questão 78

Calcule ∫ ∫ S F → ⋅ n →   d S , sendo F → ( x , y , z ) = 𝑥 𝑦 𝑖 ⃗   +   𝑦 𝑧 𝑗 ⃗   +   𝑧   2 𝑘 ⃗ , S a fronteira de   𝐵   =   { ( 𝑥 ,   𝑦 ,   𝑧 )   ∈   ℝ 3   | 0   ≤   𝑥   ≤   1 ,   0   ≤   𝑦   ≤   𝑥 ,   0   ≤   𝑧   ≤   4 } e 𝑛⃗ a normal que aponta para fora de B.

Ver solução completa

Questão 79

Escolha três afirmações para avaliar em relação a ser verdadeira (V) ou falsa (F). Para cada item

apresente argumentos que fundamentem sua avaliação.

i. Se rot F = 0, então o trabalho de F ao mover uma partícula ao longo de uma uma curva C que liga o

ponto P0 a P1 será sempre zero.

Ver solução completa

Questão 80

Escolha três afirmações para avaliar em relação a ser verdadeira (V) ou falsa (F). Para cada item

apresente argumentos que fundamentem sua avaliação.

ii. Se div F = 1, então o fluxo do campo vetorial F sobre uma superfície S, fechada e simples, coincide com o volume do sólido cuja fronteira é S.

Ver solução completa

Questão 81

Escolha três afirmações para avaliar em relação a ser verdadeira (V) ou falsa (F). Para cada item

apresente argumentos que fundamentem sua avaliação.

iii. O teorema de Green sempre relaciona o trabalho de F ao mover uma partícula ao longo do uma

curva fechada do plano com a área da região delimitada C, ou seja, pode-se obter a área de uma região por meio do teorema de Green.

Ver solução completa

Questão 82

Escolha três afirmações para avaliar em relação a ser verdadeira (V) ou falsa (F). Para cada item

apresente argumentos que fundamentem sua avaliação.

iv. Um campo conservativo F conserva o trabalho de mover uma partícula de um ponto P0 a P1.

Ver solução completa

Questão 83

Explicite duas estratégias para calcular ∬ s F d s , onde F x , y , z = ( y z 2 , x z 2 , x 2 + y 2 ) e S é a superfície definida por z = x 2 + y 2 tal que 0 ≤ z ≤ 1 .

Ver solução completa

Listas de Exercícios Resolvidos

Lista de Polinômio de Taylor para f(x,y)Lista de Wronskiano - Dependência e Independência LinearLista de Caso Vetorial no R³Lista de Caso AvançadoLista de Erro do Polinômio de Taylor para f(x)Lista de Caso Escalar R²Lista de Área de Superfícies de RevoluçãoLista de Limites Laterais e Existência do LimiteLista de Curvas de NívelLista de Área entre Curvas

Principais Conceitos de Cálculo

Equação da ParábolaPrimitivasEquação da ElipseCoeficiente LinearSemelhança de triângulos - FórmulaDiagrama De VennTabelas de Relações TrigonométricasTabela de DerivadasPropriedades do Logaritmo - Tabela