Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 8.2 - Ex. 5
5) Calcule onde e é a fronteira do quadradro de vértices (-1,0), (0,-1), (1,0),(0,1)
Passo 1
Queremos
Logo podemos usar o teorema de green, afinal
Uma ideia para resolvermos essa integral é usar o lado direito desse teorema
Passo 2
Sabendo que
Assim podemos calcular as derivadas parciais
Passo 3
Vamos unir todos esses pequenos cálculos na nossa integração
Ou seja 5 vezes a área da nossa região , que é a fronteira do quadradro de vértices (-1,0), (0,-1), (1,0),(0,1). OU seja nossa região é essa abaixo
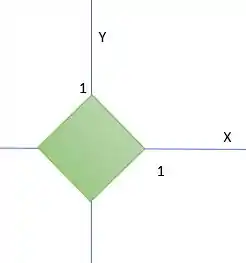
Por Pitágoras podemos descobrir que cada lado desse quadrado tem tamanho
Assim nossa integral pode se resumir a
Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Exercícios de Livros Relacionados
Sejam f ,g : a , b → R duas funções de classe C 1 tais que, para todo x em a , b , f xg x . Seja B o conjunto de todos x , y tais que f x ≤ y ≤ g x , a ≤ x ≤ b . Seja γ a fronteira de B orientada no s
Verifique a relação do exercício anterior supondo B o quadrado de vértices - 1 , - 1 , 1 , - 1 , 1,1 e - 1,1 ; γ a fronteira de B orientada no sentido anti-horário.
Verifique que ∫ γ P d x + Q d y = ∬ B ∂ Q ∂ x - ∂ P ∂ y d x d y Onde B é o triângulo de vértices 0,0 , 1,0 e 1,1 ; γ é a fronteira de B orientada no sentido anti-horário, P x , y = x 2 - y e Q x , y =
Seja B o triângulo de vértices 0,0 , 1,0 e 1,1 ; γ a fronteira de B orientada no sentido anti-horário. Verifique que ∫ γ P d x + Q d y = ∬ B ∂ Q ∂ x - ∂ P ∂ y d xd y Onde P e Q são supostas de classe
2 ) Calcule a área da região limitada pela curva x = t - sen t, y = 1 - cos t, 0≤ t ≤ 2π, e pelo eixo 0x