Exercícios de Teorema de Green - Lista de Exercícios Resolvida

Use o teorema de Green para encontrar a circulação no sentido anti-horário para o campo e a curva :

: O laço do lado direito da lemniscata .

Calcule

onde é a fronteira da região definida por

orientada no sentido anti-horário.

Use a fórmula do teorema de Green para encontrar a área da região limitada pela curva:

(Sugestão: Use )

Calcule a integral de linha do campo vetorial ao longo da curva , sendo o bordo da região definida pela interseção das seguinte regiões , , e . Além disso, assuma que é orientada no sentido horário.

Use o Teorema de Green para calcular a área da região plana do primeiro quadrante delimitada por e .

Utilize o Teorema de Green para calcular a integral de linha , onde é a fronteira da região entre e , percorrida no sentido anti-horário.

Seja . Mostre que não existe curva fechada, simples, lisa por partes tal que .

Calcule a integral de linha

Em que é a curva fronteira da região englobada pelas parábolas e com orientação positiva

Se uma circunferência de raio rola ao longo do exterior da circunferência , um ponto fixo de descreve uma curva chamada epiciclóide. Uma parametrização da epiciclóide é dada por . Nessa parametrização é uma curva fechada para . Calcule a área da região limitada pela epiciclóide .

16) Calcule as seguintes integrais:

c)

onde é a fronteira da região limitada por , e , com .

Determine o trabalho realizado pelo campo de força

Em uma partícula que inicialmente está no ponto , que se move ao longo do eixo para , e então ao longo da semicircunferência até o ponto inicial.

Calcule a integral de linha do campo vetorial ao longo da curva , sendo o bordo da região definida pela interseção das seguinte regiões , , e . Além disso, assumimos que é orientada no sentido horário.

Sejam as curvas a circunferência percorrida no sentido anti-horário, a circunferência , percorrida no sentido anti-horario e a curva formada pela união das três seguintes circunferências: , , ambas percorridas no sentido horário e percorrida no sentido anti-horário. Se onde

Então calcule .

Seja uma curva plana simples, fechada e lisa por partes, percorrida uma vez no sentido horário. Dê todos os valores possíveis para

Seja a região do plano que é interior da região e o exterior da região . Se a denota a o bordo de , orientado positivamente, , podemos afirmar que:

Questão 1. Calcule , onde e a curva consiste no segmento de reta de a , no arco de circunferência ; de a e no segmento de reta de a .

Com o auxílio do Teorema de Green, calcule as seguintes integrais de linha:

(e) é a elipse .

Calcule a integral de linha , onde é o círculo com orientação positiva.

Use o teorema de Green para calcular a integral de linha dada por

Onde é a curva de orientação positiva dada pela fronteira da região delimitada pelas parábolas e .

Considere o campo vetorial dado por , onde . Calcule , onde é a elipse , percorrida no sentido anti-horário.

Verifique o Teorema de Green, calculando as duas integrais do enunciado, para

Onde é a região interior à elipse .

Seja .

1. Use o Teorema de Green para calcular

onde é a fronteira da região englobada pelas parábolas e

Seja a integral de linha , onde

e é a fronteira do conjunto percorrida no sentido horário.

O valor de é:

Escolha uma:

a)

b)

c)

d)

e)

Use o Teorema de Green para calcular

Onde é o triângulo com vértices , e , orientado no sentido anti-horário.

Questão 3) Calcule:

1. A integral

onde é a elipse .

Use o Teorema de Green para calcular a área da região limitada pela curva plana fechada determinada pelo seguinte par de curvas: e .

Considere a integral de linha

Onde é a curva que delimita a região entre os gráficos de e .

1. Calcule usando obrigatoriamente o Teorema de Green.
2. Confira o resultado do item anterior calculando pela definição.

15) Calcule as integrais de linha diretamente e também e também pelo Teorema de Green:

b)

onde é o caminho fechado formado por , e , orientado positivamente.

15) Calcule as integrais de linha diretamente e também e também pelo Teorema de Green:

a)

onde é a circunferência unitária , , com .

Questão 4:

A curva de equação é chamada de Lemniscata de Gerono. Seu gráfico está esboçado abaixo.

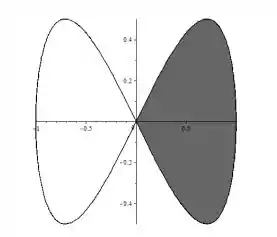
Uma parametrização para a parte da Lemniscata de Gerono que circunda a região colorida na figura acima é

1. A parametrização acima percorre a curva no sentido horário ou anti-horário? Justifique.
2. Seja uma região plana cuja fronteira é uma curva fechada e simples . Mostre que a área de pode ser calculada pela fórmula
3. Calcule a área da parte colorida na figura acima.

Calcule o trabalho do campo vetorial ao longo da curva definida em coordenadas polares por onde , e orientada com crescente.

Questão 4: Use o teorema de Green para calcular a integral de linha da função vetorial

onde é o bordo da região delimitada por e , orientado no sentido anti-horário.

Seja um campo de força sobre uma partícula. A partícula inicialmente no ponto (-2,0) se move ao longo do eixo x até (2,0) e então ao longo da semicircunferência até o ponto inicial.

1. Utilize o Teorema de Green para determinar o trabalho realizado nessa partícula pelo campo de força
2. A integral

é independendo do caminho? Justfique.

Calcule a integral

Sendo a curva a fronteira orientada positivamente da região semianular contida no semiplano superior entre as circunferências e.

Sejam e uma função não nula de classe . Considere as seguintes afirmações:

1. Se , para todo então para toda circunferência .
2. Se para todo , então para toda curcunferência vale que
3. Se é a cirncunferência percorrida uma única vez no sentido horário e é a mesma circunferência percorrida uma única vez no sentido anti-horario, então

Para toda função como acima:

Considere a curva plana orientada definida pela parametrização

Seguida do segmento de a e do segmento de a . Calcule a integral de linha

Considere a integral de linha

Onde é a fronteira da região do primeiro quadrante limitada pelas circunferências e e é o campo vetorial definido por

Calcule usando obrigatoriamente o teorema de Green

Diga se as afirmações seguintes são verdadeiras ou falsas. Justifique.

Se é uma curva simples, fechada, orientada positivamente e que limita uma região plana com área e se , para , então é sempre verdade que

Mostre que

Para qualquer curva , fechada, simples, lisa (ou regular) por partes, cujo traço não intersecta os eixos e dos e orientada no sentido positivo, e para qualquer função de classe .

Sugestão: Aplique o Teorema de Green. Justifique

Considere o caminho que delimita a região do plano limitada pelas linhas de equação e e percorrido no sentido anti-horário.

1. Usando a definição, calcule a integral de linha

(não precisa resolver a integral)

2. Calcule a integral do item , agora usando o teorema de Green

Use o Teorema de Green para calcular a área da região plana do primeiro quadrante delimitada por e .

Calcule, usando o Teorema de Green, a seguinte integral de linha

onde a curva é a fronteira da região delimitada pelas parábolas

Calcule a integral:

Onde é o quadrado cortado no primeiro quadrante pelas retas e

12. Calcule ,onde é o gráfico de , de a .

Se é a região interior a elipse e exterior à circunferência , calcule a integral de linha

Onde está positivamente orientada.

Calcule as seguintes integrais de linha:

Onde é o triângulo de vértices , , , percorrido no sentido anti-horário.

Calcule as seguintes integrais de linha:

Onde é o círculo unitário com centro na origem, percorrido no sentido anti-horário.

Considere o campo plano

e os caminhos:

quadrado de vértices e com orientação anti-horária;

circunferência unitária com orientação horaria.

Calcule

Sugestão: use o Teorema de Green (generalizado).

(Cap.16.4 - Exercício 1) Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green.

é o círculo com centro na origem e raio

(Capítulo 16.4 – Exercício 5) Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva.

,

é o triângulo de vértices

(Cap.16.4 - Exercício 28) Calcule , onde e é a fronteira positivamente orientada de uma região que tem área 6.

(Cap.16.4 - Exercício 2) Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green.

é o retângulo com vértices

(Cap.16.4 - Exercício 11) Use o teorema de Green para calcular . (Verifique a orientação da curva antes de aplicar o teorema.)

, é o triângulo de

16) Calcule as seguintes integrais:

d)

onde é a fronteira da região limitada por e .

16) Calcule as seguintes integrais:

b)

onde é formada por , e .

Questão 1. Use o Teorema de Green e calcule a integral de linha ao longo da orientação positiva da curva dada.

(a) , é o quadrado com lados , , e ;

Questão 1. Use o Teorema de Green e calcule a integral de linha ao longo da orientação positiva da curva dada.

(b) , é o limite da região entre as curvas e ;

Questão 1. Use o Teorema de Green e calcule a integral de linha ao longo da orientação positiva da curva dada.

(c) , é a elipse

Questão 2. Use o Teorema de Green para calcular . (Verifique a orientação da curva antes de aplicar o teorema.

(a) , é o triângulo de para , para e para ;

Questão 2. Use o Teorema de Green para calcular . (Verifique a orientação da curva antes de aplicar o teorema.

(b) , é o círculo com orientação positiva;

20) Seja de classe , tal que . Considere o campo . Calcule onde é a curva formada por e .

Calcule , em que

E é a fronteira orientada positivamente de uma região que tem área .

(Cap.16.4 - Exercício 7) Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva.

é o limite da região englobada pelas parábolas e

Calcule a integral de linha onde é o bordo da região delimitada por e , orientado no sentido anti-horário.

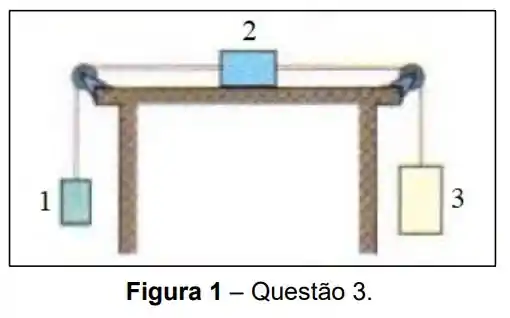
Na figura a seguir temos a imagem de três caixas, ligadas entre si por cordas, de massas desprezíveis, que passam por polias sem atrito. O bloco 2 está sobre uma superfície com coeficiente de atrito cinético de e as massas das caixas são , e . Ao liberarmos as caixas para se movimentarem, qual a tensão na corda da esquerda?

(Cap.16.4 - Exercício 4) Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green.

Questão 5: Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva.

Onde é a fronteira da região englobada pelas parábolas e .

Calcule a integral de linha , C é o retângulo com vértices (0, 0) , (3, 0) , (3, 1) e (0, 1) por dois métodos:

b) utilizando o Teorema de Green;

Seja o arco de círculo com centro na origem e raio 2 orientado no sentido anti-horário do ponto até o ponto e seja tal que