Considere a função , e . Seja um real dado.
Calcule a área do retângulo limitado pela reta , , e , onde é um natural dado.
Passo 1
A seguir temos um esboço do retângulo mencionado:
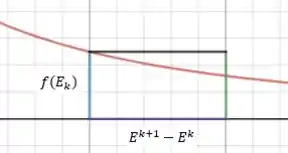
A base do retângulo é e a altura é . A área do retângulo é
Logo,
Podemos escrever
Passo 2
Mas lembre-se que
Assim,
Portanto,
Com isso, obtemos