Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.10 - Ex. 11

É dada uma função g .

a) Determine os valores de k tais que lim x → k ⁡ g ( x ) < 0 .

b) Ache todos os intervalos abertos a ,   b que contêm um determinado valor de k que satisfaça a parte a) tais que g ( x ) < 0 para todo x ≠ k em a ,   b .

c) Faça um esboço do gráfico de g e mostre no gráfico a interpretação geométrica dos resultados das partes a) e b).

g x = 2 x 2 + x - 6 2 x 2 + 11 x + 14

Passo 1

lim x → k ⁡ g ( x ) = 2 k 2 + k - 6 2 k 2 + 11 k + 14 < 0

Aplicando o caso 2 temos que

2 k 2 + k - 6 < 0   e   2 k 2 + 11 k + 14 < 0

2 k - 3 k + 2 < 0   e   k + 2 2 k + 7 > 0

Aplicando o caso 1 em 2 k - 3 k + 2

2 k - 3 < 0   e   k + 2 > 0

k < 3 2   e   k > - 2

Aplicando o caso 2 em k + 2 2 k + 7

2 k + 7 > 0   e   k + 2 < 0

k > - 7 2   e   k < - 2

Assim lim x → k ⁡ g ( x ) < 0 sempre que k estiver nos intervalos - 7 2 , - 2 e - 2 , 3 2

Resposta

a) lim x → k ⁡ g x < 0 sempre que k estiver nos intervalos - 7 2 , - 2 e - 2 , 3 2

b) Como g ( x ) - 7 2   < x < - 2 ou - 2   < x < 3 2 , os intervalos abertos requeridos a ,   b contendo k e tais que g ( x ) - 7 2 ≤ a < k e k < b ≤ - 2 ou - 2 ≤ a < k e k < b ≤ 3 2 .

c)

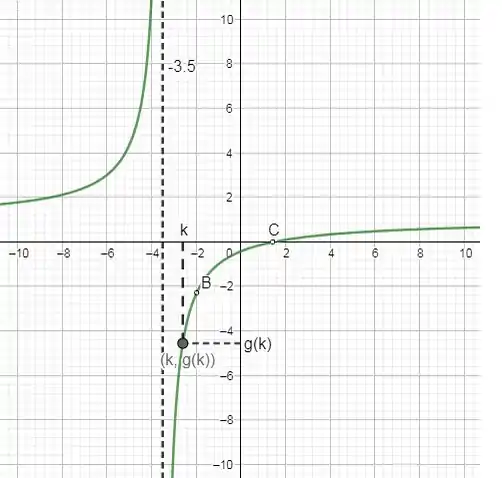
Os pontos B e C marcam onde há descontinuidade quando x = - 2 e x = 3 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine, se existirem, os pontos onde as seguintes funções não são contínuas. f x = 1 1 + 2 sen ⁡ x
Prove que se f x e g x são contínuas em x 0 = 3 , também o são f + g e f ⋅ g .
Construa o gráfico e analise a continuidade das seguintes funções: f x = x 3 + 3 x 2 - x - 3 x 2 + 4 x + 3
Investigue a continuidade nos pontos indicados:f (x) = {[[(x^2 - 4)/(x - 2) , x != 2],[0 , x = 2]]) e m x = 2
Determine, se existirem, os valores de x ∈ D f , nos quais a função f x não é contínua. f x = cos ⁡ x x + π