Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.6 - Ex. 98

Determine a área entre a curva y = t g (x) e o eixo x de x = - (pi)/(4) até x = (pi)/(3) .

Passo 1

Perceba que inicialmente esboçar o gráfico para identificar qual a função que está acima e qual está abaixo, parece uma boa ideia. Já que pela definição

A = int_a^b [f (x) - g (x)] d x

Ou seja, área da região entre as curvas, é a integral da função de cima f ( x ) menos a função de baixo g (x) .

Passo 2

Esboçando o gráfico da função, seja por um software, ou substituindo alguns valores em cada umas das funções para obter pontos, teremos um gráfico como esse ou parecido,

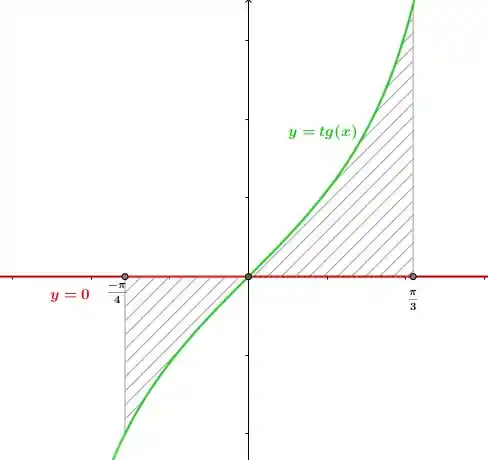
Onde, pelo que podemos ver em parte de (- pi)/(4) até 0 y = 0 é a função que está por cima , y = t g ( x ) é a função que está por baixo e a parte hachurada é região que desejamos calcular a área. Porém a partir de 0 até (pi)/(3) , isso muda e y = t g (x) passa a ser a função que está por cima e y = 0 é a função que está por baixo. Sendo assim a integral será :

int_(- (pi)/(4))^0 0 - t g (x) d x + int_0^((pi)/(3)) t g (x) - 0 d x

Cujos limites de integração foram obtidos, a partir de onde a parte hachurada começa até onde ela termina, sendo interrompida no ponto de intersecção entre as duas curvas. Lembrando que, trabalhar com y = 0 é o mesmo que está com o eixo x .

Passo 3

Já que já encontramos a “cara” integral que para determinar a área, então vamos partir para os cálculos e ver quando essa integral vai dar. Mas para não nos confundirmos vamos calcular cada uma separadamente,

int_(- (pi)/(4))^0 0 - t g (x) d x + int_0^((pi)/(3)) t g (x) - 0 d x

Resolvendo a integral 1

int_(- (pi)/(4))^0 0 - t g (x) d x = int_(- (pi)/(4))^0 - t g (x) d x = - int_(- (pi)/(4))^0 t g (x) d x =

- int_(- (pi)/(4))^0 t g (x) d x = - int_(- (pi)/(4))^0 (s e n (x))/(cos (x)) d x

Utilizando substituição, suponha que u = c o s ( x ) então d u = - s e n ( x ) d x => d x = (1)/(- s e n (x)) d u .Além disso quando x = - (pi)/(4) => u = cos (- (pi)/(4)) = - cos ((pi)/(4)) = - (sqrt(2))/(2) e quando x = 0 => u = cos (0) = 1 . Sendo assim

- int_(- (pi)/(4))^0 t g (x) d x = - int_(- (pi)/(4))^0 (s e n (x))/(cos (x)) d x

= - int_(u = - (sqrt(2))/(2))^(u = 1) (s e n (x))/(u) . (1)/(- s e n (x)) d u = + int_(u = - (sqrt(2))/(2))^(u = 1) (s e n (x))/(u) . (1)/(s e n (x)) d u

- int_(- (pi)/(4))^0 t g (x) d x = int_(- (pi)/(4))^0 (s e n (x))/(cos (x)) d x = int_(u = - (sqrt(2))/(2))^(u = 1) (s e n (x))/(u) . (1)/(s e n (x)) d u

= int_(u = - (sqrt(2))/(2))^(u = 1) (1)/(u) d u = ln |u| (​|_(u = - (sqrt(2))/(2))^(u = 1)

Usando o Teorema Fundamental do Cálculo Parte II,

- int_(- (pi)/(4))^0 t g (x) d x = ln |u| (​|_(u = - (sqrt(2))/(2))^(u = 1) = [ln |1| - ln |- (sqrt(2))/(2)|]

= [ln (1) - ln ((sqrt(2))/(2))] = 0 - ln ((sqrt(2))/(2)) = - ln ((sqrt(2))/(2))

Resolvendo a integral 2

int_0^((pi)/(3)) t g (x) - 0 d x = int_0^((pi)/(3)) t g (x) d x

Utilizando os mesmas regras usadas para resolver a integral 1, teremos

int_0^((pi)/(3)) t g (x) d x = int_0^((pi)/(3)) (s e n (x))/(cos (x)) d x = - int_(u = 0)^(u = (1)/(2)) (s e n (x))/(u) . (1)/(s e n (x)) d u = int_(u = 0)^(u = (1)/(2)) (1)/(u) d u = - ln |u| (​|_(u = 0)^(u = (1)/(2)) = - [ln |(1)/(2)| - ln |1|] = - [ln (1)/(2) - ln 1] = - [ln (1)/(2) - 0] = - ln ((1)/(2))

Portanto,

int_(- (pi)/(4))^0 0 - t g (x) d x + int_0^((pi)/(3)) t g (x) - 0 d x = - ln ((sqrt(2))/(2)) - ln ((1)/(2)) = - [ln ((sqrt(2))/(2)) + ln ((1)/(2))]

Usando o Teorema Fundamental do Cálculo Parte II,

Resposta

Área da região entre y = 0 , y = t g ( x ) , quando - (pi)/(4) <= x <= (pi)/(3) é igual à - [ln ((sqrt(2))/(2)) + ln ((1)/(2))]

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área das regiões delimitadas pelas curvas e retas y 2 = 4 x , y = 4 x - 2
Determine a área da região cortada do primeiro quadrante pela curva x 1 2 + y 1 2 = a 1 2
Determine a área entre a curva y = 1 x e o eixo x de x = 10 até x = 20 é a mesma área entre a curva e o eixo x de x = 1 até x = 2 .
Determine a área total da região delimitada pela curva = s e n x , y = c o s x0 ≤ x ≤ 3 π 2
Determine a área entre a curva y = 1 x e o eixo x de k a até k b é a mesma área entre a curva e o eixo x de x = a até x = b . ( 0ab , k0 ).