Determine a área da superfície.
A parte do cilindro que está acima do retângulo com vértices , , e .
Passo 1
E aiii galerinha, tudo na paz? Bora pra mais uma!!!
O enunciado pede para calcularmos a área da superfície. Essa superfície é a parte do cilindro:
que está acima do retângulo com vértices:
Como resolvemos essa?
Primeiro vamos lembrar como calculamos a área de uma superfície. Para isto, basta resolver a seguinte integral:
Onde, .
Portanto, precisamos calcular primeiramente as derivadas parciais de em função de e de para só depois resolvermos as integrais.
Observe a expressão dada. Conseguimos obter uma expressão, basta isolar o z. Logo, vamos ter:
Para determinar nossos intervalos de integração, vamos esboçar a região retangular. Assim vamos saber os intervalos de variação de e .
Agora ficou fácil em pessoal!!! Bora lá resolver!
Passo 2
Vamos determinar primeiramente as derivadas parciais de .
Sendo assim,
Portanto, devemos resolver a seguinte integral:
Simplificando a expressão dentro da raiz quadrada, vamos ter:
Passo 3
Como estamos em uma região retangular com vértices:
Vamos esboçar essa região no plano para identificar os intervalos de e .
Esboçando, temos:
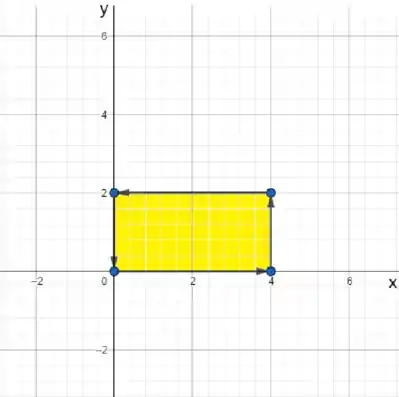
Observe que os intervalos de x e y são:
Agora é so montar a integral pessoal.
Tá mas qual eu coloco primeiro para integrar??
Aqui vale a gente lembrar do Teorema de Fubini, que tanto faz a ordem de integração. Porque estamos com ambos os limites de integração em numerais, então tanto faz qual vamos integrar primeiro.
Portanto, basta resolvermos a seguinte integral:
Passo 4
Lembre-se, sempre começamos integrando de dentro para fora.
Vamos começar integrando em dx. Integrando vamos ter:
Aplicando os limites de integração, temos:
Restou uma integral simples em . Aqui vamos ajustar um pouco a integral, porque conhecemos uma integral com essa cara.
Ajustando, temos:
Faça uma comparação com a integral abaixo:

Assim, concluímos que:
Aplicando os limites de integração, vamos ter como resposta: