Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.1 - Ex. 31
Encontre a área exata sob a curva cosseno de até , onde . (Use um sistema de computação algébrica para calcular a soma e o limite.) Em particular, qual é a área, se ?
Passo 1
Opa! Bora pra mais uma questão?!
A gente precisa calcular a área exata sob a curva de de até , onde . Pra isso vamos primeiro ver como é essa curva:
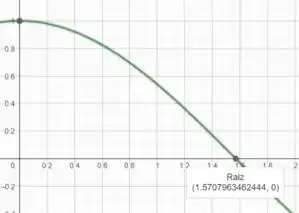
O ponto é a raiz da curva, aproximadamente igual a . Mas esse gráfico é só pra deixar o problema mais palpável mesmo, a fórmula que iremos usar pra calcular a área é essa daqui:
Na prática, vamos separar a região abaixo da curva em retângulos com altura e largura . Assim, cada um desses retângulos terá área e quando fizermos a soma de todos os retângulos formados abaixo da curva, vamos cair na fórmula de .
Podemos definir como:
Onde é o intervalo da área abaixo da curva e quando fazemos estamos dividindo a região abaixo da curva em infinitos retângulos.
Enfim! Vamos começar!
Passo 2
Para usar a fórmula acima precisamos de duas coisas . Começando pelo espaçamento:
Conhecemos , que é igual a zero, mas está variando entre e , então:
Agora precisamos descobrir qual o , utilizando a seguinte fórmula:
Vamos substituir:
Assim podemos dizer que:
Agora vamos substituir os dados que conseguimos na fórmula da área:
Tranquilo até aqui?
Passo 3
Agora vamos utilizar o sistema de computação algébrica para calcular a soma:
O programa também é capaz de simplificar este limite:
Sendo assim,
Pra acabar vamos calcular quando
É isso! O que achou? Responde Aí!