Integrais

Fala aí, nós somos o Responde Aí, e o nosso objetivo aqui hoje é fazer você entender que

NÃO PRECISA MAIS SE ASSUSTAR COM AS FAMOSAS INTEGRAIS!

O que são integrais?

Eu sei que o nome é diferente, mas a integral basicamente representa o valor de uma área.

E você pode estar se perguntando: Pra que eu vou usar algo mais elaborado como as integrais para calcular uma área se eu já sei calcular áreas pelas fórmulas?

E você nunca se perguntou de onde saíram essas fórmulas? Essas fórmulas surgem através do cálculo de uma integral e facilitam muito nossa vida, porém tem áreas mais complexas, que não possuem um formato muito bem definido e que a gente não consegue encontrar uma fórmula geral e por isso precisamos utilizar as integrais para calculá-las.

Por exemplo, calcular a área embaixo da curva entre os pontos e :

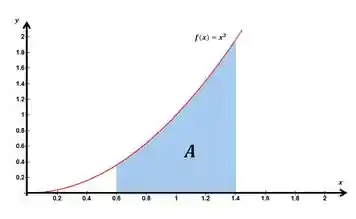
Não temos nenhuma fórmula para calcular essa área, então usaremos a integral e a notação é a seguinte:

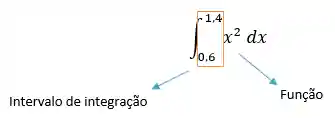
Essa integral, que representa a área sob uma curva, é chamada de integral definida.

Mas, ainda temos a chamada integral indefinida que é aquela que não possui intervalo de integração e por isso ela não representa a área sob uma curva. Na verdade, a integral indefinida resultará em uma função, que é chamada de primitiva da função que se está integrando:

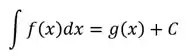
Onde:

• é uma função conhecida;
• é a primitiva de

Mas o que significa dizer que é primitiva de ? Quer dizer que quando é derivada encontramos como resposta. Ou seja, a integral é a operação inversa da derivação.

ATENÇÃO!!! Sempre que resolver uma integral indefinida deve aparecer aquele no final, que é chamado de constante de integração. Essa constante aparece porque a derivada de uma constante é zero, então pode haver uma família de funções do tipo tal que a derivada será igual a , justamente porque o valor da constante não fará diferença na derivada porque derivada de constante é zero.

Como calcular integrais?

E agora você pode estar pensando: Beleza, a integral é a operação inversa da derivação, então para eu calcular a integral eu tenho que pensar o contrário do que eu pensava para fazer a derivada? É basicamente isso!

MAS existe uma tabela, chamada tabela de integrais, que já tem o resultado da integral indefinida das funções mais conhecidas, e isso facilita DEMAIS a nossa vida de estudante sofrido kkkkkk. Nós temos essa tabela prontinha pra você, você pode conferir aqui: Tabela de Integrais.

Videoaula

Essa foi uma introdução muito breve de integrais.

E se você preferir, pode conferir essa introdução breve através de uma videoaula:

Dentro desse assunto tem várias outras coisas que você vai precisar estudar para arrasar nas provas e passar esse semestre de forma tranquila.

Aqui no Responde Aí, nós temos todo esse conteúdo completo e organizado, para o seu estudo ser muito mais produtivo e claro.

Confere aqui o nosso Raio-X do assunto de Integrais. É só você clicar e conferir 👇🏾