Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.5 - Ex. 43
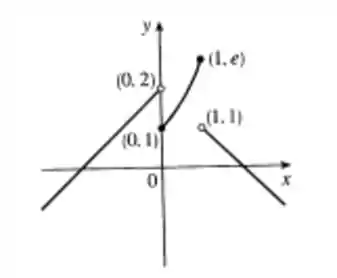
Encontre os pontos nos quais é descontínua. Em quais desses pontos é contínua à direita, à esquerda ou em nenhum deles? Esboce o gráfico de .
Passo 1
Boa galera, Yuri aqui e estarei te ajudando a resolver essa atividade.
Nesse exercício queremos encontrar os valores aonde nossa função é descontínua dentro dos intervalos dados. A nossa função é contínua ao longo do intervalo por ser um polinômio.
Para o intervalo nossa função também é contínua, por também ser um polinômio. Ao longo do intervalo a função também é contínua, por ser uma função exponencial. Funções polinomiais e exponenciais são definidas em todos os pontos.
Então nosso interesse vão ser os pontos de “colagem” entre funções, ou seja, os extremos dos intervalos.
Passo 2
Agora vamos olhar para os pontos extremos dos intervalos. Temos o valor em e em . Aplicamos assim o limite tendendo a em e tendendo a em .
Assim, como os limites laterais são diferentes, a função é descontínua no ponto .
Fazemos o mesmo para o valor no intervalo de e .
E
Portanto, nossa função é descontínua no ponto pois os limites laterais são diferentes.
Passo 3
Como e , nossa função é contínua pela direita no ponto e pela esquerda no .
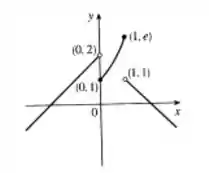
Resposta
Assim, podemos concluir que a nossa função é descontínua nos pontos e no ponto . No ponto , a função é contínua à direita e no ponto , a função é contínua pela esquerda. O gráfico da nossa função fica assim:
