Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.2 - Ex. 5a
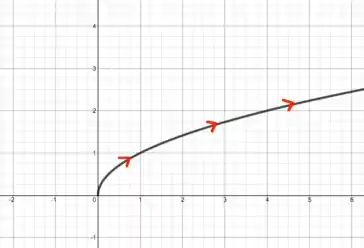
- Esboce o gráfico da curva plana com a equação vetorial dada.
- Encontre .
- Esboce o vetor posição e o vetor tangente para o valor dado de .
Passo 1
Galera, a curva é dada pela seguinte equação:
Aqui, temos que e . Queremos traçar o gráfico dessa curva. O que a gente pode fazer aqui, é nos aproveitar da relação entre e e colocarmos essa curva em coordenadas cartesianas.
Para resolver essa atividade, a gente vai relembrar nossos tempos de escola. Vamos colocar alguns valores de na função , e após isso teremos os pontos , iremos então plotar esses pontos utilizando o GeoGebra e assim teremos o nosso gráfico.
Passo 2
Se substituirmos no , temos:
Essa equação é uma parábola horizontal com o vértice na origem, quando . Porém, como não pode ser negativo, nós pegamos apenas a parte de cima.
Talvez não seja necessário desenhar setas, mas é legal para mostrar a direção para onde cresce.
“Mas como definimos a direção das setas?”
você deve estar se perguntando.
Bom, sabemos que e . Conforme aumenta, ambos e aumentam. Então, as setas apontam na direção em que e aumentam.
Passo 3
Agora vamos aos pontos:
Para
Para
Para
Para
Para
Então plotando o gráfico com esses e outros pontos, a gente tem o seguinte comportamento:
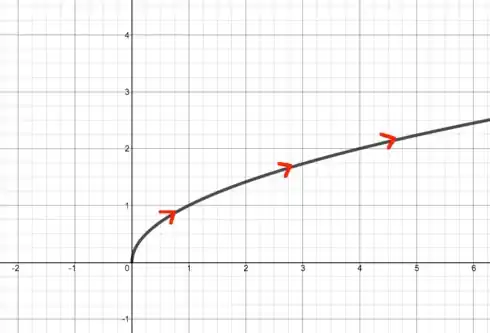
Resposta
O gráfico é:
