Exercícios de Produto Escalar ou Interno - Lista de Exercícios Resolvida

Ache tal que e é ortogonal a e a . Dos “”s encontrados, qual o que forma ângulo agudo com o vetor ?

Determinar o vetor ortogonal ao vetor e colinear ao vetor .

Calcular o módulo dos vetores e , sabendo que e o ângulo entre e é de .

Sejam os pontos e Pede-se:

1. Mostrar que o triangulo é retângulo em
2. Calcular a medida da projeção do cateto sobre a hipotenusa .
3. Determinar o pé da altura do triangulo relativa ao vértice .

Mostre que

Calcular o ângulo entre os vetores e

Determinar um vetor ortogonal aos vetores e .

Determine o valor do produto interno entre os vetores e .

Dados os vetores e e os pontos e , determinar o valor de tal que .

Sabendo que o vetor forma um ângulo de com o vetor determinado pelos pontos e , calcular .

Mostrar que se e são vetores, tal que é ortogonal a , então .

Determinar o vetor , paralelo ao vetor , tal que

Considere as seguintes afirmações

Então está certo o que se afirma em:

Suponha que , , e considere as afirmações seguintes:

Então está correto apenas o que se afirma em:

Considere o espaço vetorial munido do produto interno definido por:

Se

E são tais que , então é igual a:

Considere a função definida por:

Assinale a alternativa correta:

não é um produto interno em , pois existem e tais que

não é um produto interno em , pois existem não nulo tal que

é um produto interno em

não é um produto interno em , pois existem tais que

não é um produto interno em , pois existem tais que

Considere os vetores do espaço vetorial , munido do produto interno usual. Se é tal que , então é igual a

Seja V um espaço vetorial com produto interno e sejam . Então se, e somente se,

Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmação for falsa, exiba explicitamente um contraexemplo.

(c) Se e são vetores de , então .

Sejam tais que

e sejam ortogonais a e a medida do ângulo entre e seja igual a .

Temos que é igual a:

A questão da era: “Sejam vetores de . Suponha que são vetores linearmente independentes e que . Os vetores são linearmente independentes? Justifique.” A resposta do Joãozinho foi:

Escreva a definição de .

Qual hipótese do enunciado da questão o Joãozinho não usou? Dê um exemplo onde, sem essa hipótese são linearmente dependentes

Escreva uma demonstração correta e completa que os vetores são linearmente independentes começando por:

“Sejam escalares tais que ”

Sejam tais que

Então, é igual a

a)

b)

c)

d)

e)

Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmação for falsa, exiba explicitamente um contraexemplo.

(b) Se e são vetores não nulos e tais que , então .

(c) Se e são vetores tais que , então ou .

Considere o produto interno usual de R4 e sejam e . Calcule a distância de u a v.

(a) 1

(b) 6

(c) √6

(d) −1

Considere o vetor e a reta passando pela origem cuja direção é dada pelo vetor . O vetor de mais próximo de possui norma igual a:

Considere o espaco vetorial de munido do seu produto interno usual e seja o subespaço de definido por:

Temos que é igual a:

(a)

(b)

(c)

(d)

(e)

Sejam vetores tais que sejam ambos ortogonais a

E a medida do ângulo entre seja igual a . Temos que é igual a:

Considere o tetraedro regular de aresta unitária

O valor de

Sejam vetores distintos. Assinale a alternativa contendo uma afirmação FALSA.

Sejam tais que , e o ângulo entre e mede . Se é a medida do ângulo entre e , então é igual

Sabe-se que é um vértice de um quadrado que possui diagonal contida na reta r: . Então é correto afirmar que existe um outro vértice do quadrado com a+b+c igual a:

Sejam , vetores não-nulos. Considere as seguintes afirmações a respeito desses três vetores:

, então

, então , ,

1. Considere

1. Determine um vetor paralelo a , de comprimento .

Considere no espaço um cubo cujos vértices são , em que e são faces desse cubo, como ilustrado na figura abaixo:

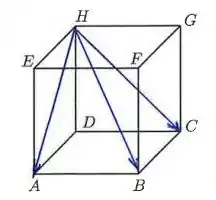
Considere também os seguintes sistemas de coordenadas em :

Se for o ponto cujos coordenadas no sistema são , então as coordenadas de no sistema serão:

a)

b)

c)

d)

e)

Sejam tais que e tais que a medida do ângulo entre e seja igual a . Temos que é igual a:

a)

b)

c)

d)

e) ;

Considere as seguintes afirmações:

para quaisquer , vale que

para quaisquer , vale que:

para qualquer base ortonormal positiva vale que:

Assinale a alternativa correta:

a) apenas as afirmações e são verdadeiras;

b) apenas as afirmações E são verdadeiras;

c) todas as afirmações são verdadeiras;

d) apenas as afirmações e são verdadeiras;

e) apenas a afirmação é verdadeira.

Considere as seguintes afirmações:

se for um sistema de coordenadas em em que é uma base ortonormal de , então a área do triângulo de vértices e será igual a .

se forem vetores não nulos e paralelos, então:

para qualquer

a matriz

É invertível e sua inversa é

Assinale a alternativa correta:

a) todas as afirmações são verdadeiras;

b) apenas a afirmação é verdadeira;

c) apenas as afirmações e são verdadeiras;

d) apenas as afirmações e são verdadeiras;

e) apenas as afirmações e são verdadeiras.

Sejam tais que , , e tais que e são, ambos, ortogonais a . Se o ângulo entre e mede , então é igual a

Seja uma base ortonormal de . Considere os vetores e , em que são números reais. Sabendo que e que o ângulo entre e mede , é correto afirmar que é igual a

a)

b)

c)

d)

e)

f)

Seja uma base de tal que

- ,

- o ângulo entre e mede

- é ortogonal tanto a quanto a

Considere os vetores e . Então, o produto escalar é igual a

a)

b)

c)

d)

e)

Sabendo que e são vetores de tais que , o ângulo entre e mede e é ortogonal tanto a quanto a , é correto afirmar que é igual a