Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 4.2 - Ex. 5

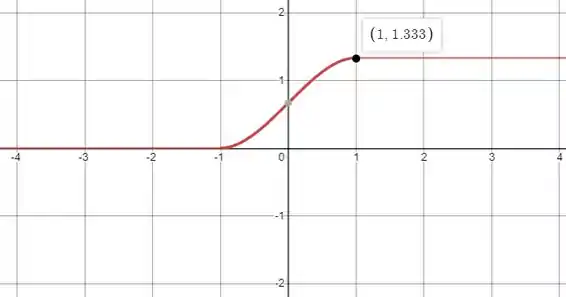
Esboce o gráfico de

F (x) = int_(- oo)^x f (t) d t

onde

f (t) = {[[0,s,e,,|t|,>,1],[1,-,t^2,s,e,,|t|,<=,1]])

Passo 1

Primeiramente, vamos olhar para f ( x ) graficamente

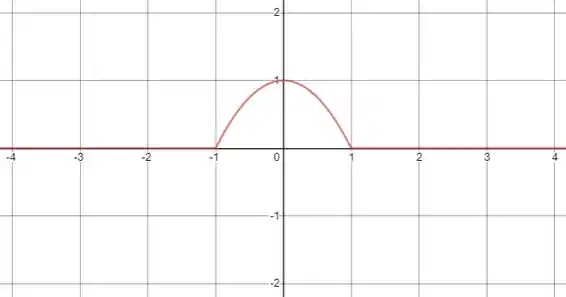
Podemos separar então a nossa função F ( x ) em três etapas, para x < - 1 , para - 1 <= x <= 1 e x > 1 . Essa separação se deve pela própria separação da função f ( t ) .

Passo 2

Então vamos analisar cada etapa:

Se x < - 1

F (x) = int_(- oo)^x f (t) d t = int_(- oo)^x 0 d t = 0

Se - 1 <= x <= 1

F (x) = int_(- oo)^x f (t) d t = int_(- oo)^(- 1) 0 d t + int_(- 1)^x ( 1 - t^2 ) d t

= int_(- 1)^x ( 1 - t^2 ) d t = [t - (t^3)/(3)]_(- 1)^x

= x - (x^3)/(3) - (- 1) + ((- 1)^3)/(3)

= x - (x^3)/(3) + (2)/(3)

Se x > 1

F (x) = int_(- oo)^x f (t) d t = int_(- oo)^(- 1) 0 d t + int_(- 1)^1 ( 1 - t^2 ) d t + int_1^x 0 d t

= int_(- 1)^1 ( 1 - t^2 ) d t = [t - (t^3)/(3)]_(- 1)^1

= 1 - (1^3)/(3) - (- 1) + ((- 1)^3)/(3)

= (4)/(3)

Podemos então definir a função como

F (x) = {[[x,-,(x^3)/(3),+,(2)/(3),s,e,,-,1,<=,x,<=,1],[(4)/(3),s,e,,x,>,1],[0,s,e,,x,<,-,1]])

Passo 3

Vamos então esboçar o gráfico de F ( x ) no plano:

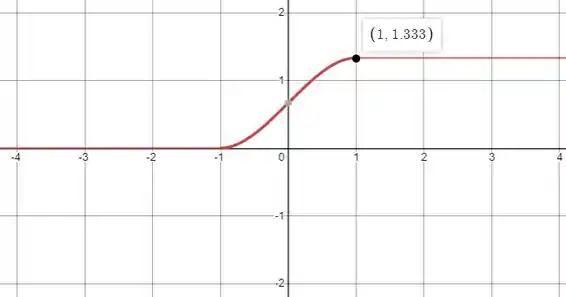
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver as seguintes integrais usando a técnica de integração por partes. ∫ ln ⁡ ( x 2 + 1 ) d x
Resolver as seguintes integrais usando a técnica de integração por partes. ∫ x c o s 2x d x
Resolver as seguintes integrais usando a técnica de integração por partes. ∫ x 3 1 - x 2d x
Resolver as seguintes integrais usando a técnica de integração por partes. ∫ x s e n5 xd x
Resolver as seguintes integrais usando a técnica de integração por partes. ∫ x 5 e x 2 d x