7. Mesmo exercício que o anterior onde é dada por .
Passo 1
Letra (a)
O esboço pedido por ser representado por:
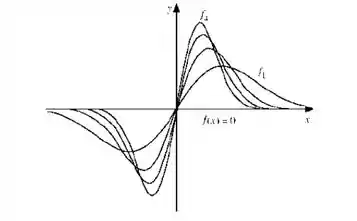
Passo 2
Letra (b)
Seja
Se uniformemente em dado , existiria tal que, para todo . Em particular, para deveríamos ter
Como , então não converge uniformemente em
Passo 3
Letra (c)
Temos
Portanto,
Resposta
- Figura
- Demonstração
- Demonstração