Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.Revisão - Ex. 15
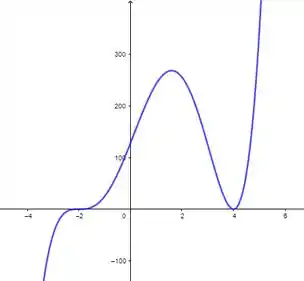
Nos exercícios de 13 a 32, faça um esboço do gráfico da função f dada, determinando primeiro o seguinte: os extremos relativos de f; os pontos de inflexão do gráfico; os intervalos nos quais f é crescente e aqueles onde f é decrescente; onde o gráfico é côncavo para cima e onde é côncavo para baixo; a inclinação das tangentes inflexionais, assíntotas horizontal, vertical e oblíqua, se existirem.
Passo 1
Seja . Vejamos que as raízes da função são .
Passo 2
Calculando utilizando a regra do produto, teremos:
As raízes de serão . Dessa maneira, teremos:
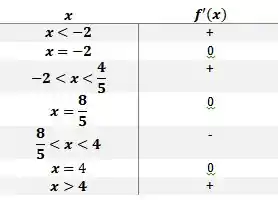
Passo 3
Calculando utilizando a regra do produto, teremos que:
Para achar as raízes, pela Fórmula de Bhaskara, teremos:
Dessa forma, teremos que:
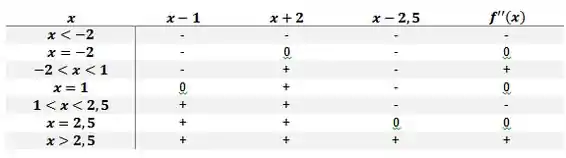
Logo, temos que a inclinação das tangentes inflexionais serão .
Passo 4
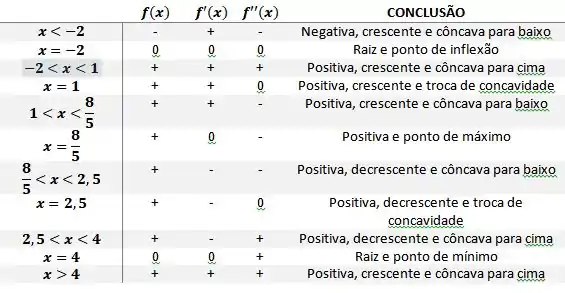
Passo 5
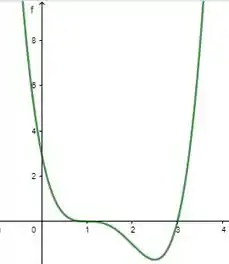
Com os dados acima coletados e alguns pontos calculados, teremos:
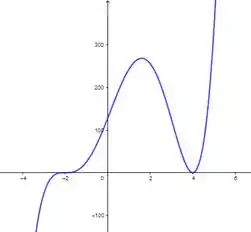
E os valores de máximo e mínimo relativos são, respectivamente, e
Resposta
Os extremos relativos de .
Os pontos de inflexão de
A função é crescente em e decrescente em .
O gráfico é côncavo para baixo em e côncavo para cima em .
A inclinação das tangentes inflexionais são .
Gráfico:
