Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.7 - Ex. 41

  1. Dê uma expressão integral para o momento de inércia I z em torno do eixo z de uma folha fina no formato da suerfície S , se a função densidade é ρ .
  2. Determine o momento de inércia em torno do eixo z do funil do exercício 40 .

Passo 1

Oi galera, tudo bem?

Temos dois itens para calcular, o item (a) e o (b). No item (a) devemos achar uma expressão de integral para o momento de inercia I z em torno do eixo z de uma folha fina no formato da suerfície S , se a função densidade é ρ .

Já no item (b), achar o momento de inercia em torno do eixo z do funil do exercício 40.

Vamos fazer com calma essa, beleza!

Para o item (a), vamos lembrar que o momento de inercia pode ser escrito como:

I = ∬ S r 2 d m

Onde r é a distância da massa ao eixo de referência.

O segredo agora é você achar uma relação para   r em função das coordenadas ( x , y , z ) e lembrar que dm pode ser escrito como:

d m = ρ ( x , y , z ) d S

Depois é só substituir na integral.

Já para o item (b), vamos primeiro lembrar dos dados do exercício 40.

Tínhamos que a equação do funil é:

z = x 2 + y 2 ,       1 ≤ z ≤ 4

Com densidade:

ρ = 10 - z

Vamos tomar como referencia esse formato de integral para resolução:

Onde o nosso vetor normal n vai ser:

n → = | r → x × r → y |

Repare que temos o modulo do produto vetorial, entre as derivadas da parametrização r em relação a x e y . Antes lembre-se de achar uma parametrização para esse funil.

Um dia bem importante: Repare que a projeção do funil no plano x y é uma série de círculos com raios que variam entre 1 e 4 , pois 1 ≤ z ≤ 4 . Então a região pode ser dada, em coordenadas polares da seguinte forma:

1 ≤ r ≤ 4 0 ≤ θ ≤ 2 π   d A = r d r d θ

Com todas essas informações, você já pode começar a resolver!

Vamos nessa!

Passo 2

Começando pelo item (a).

Sabemos que o momento de inercia pode ser escrito como:

I = ∬ S r 2 d m

Onde r é a distância da massa ao eixo de referência. Repare na imagem abaixo, podemos ver que r é a distância da massa d m até o eixo z , e por analise de Pitágoras no triangulo retângulo temos que:

r 2 = x 2 + y 2

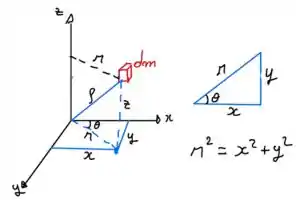
Sabemos que o diferencial d m pode ser rescrito como:

d m = ρ ( x , y , z ) d S

Então colocando no integrando temos:

I z = ∬ S x 2 + y 2 ρ ( x , y , z ) d S

Essa é a representação em integral do momento de inercia em relação ao eixo z .

Passo 3

Agora vamos para o item (b).

Já temos uma expressão para o momento de inercia em relação ao eixo z:

I z = ∬ S x 2 + y 2 ρ ( x , y , z ) d S

Sabemos do exercício 40 , que:

z = x 2 + y 2 ,       1 ≤ z ≤ 4

Com densidade:

ρ = 10 - z

Assim, podemos usar a densidade como:

ρ = 10 - x 2 + y 2

Mas lembre-se, que a integral não é exatamente assim, temos que ajustar o termo d S . Vai ficar assim:

I z = ∬ S x 2 + y 2 ρ ( x , y , z ) n → d A

Onde, o vetor normal vai ser dado por:

n → = | r → x × r → y |

Onde r → é a superfície parametrizada. Vamos obter então!

Como temos que z = x 2 + y 2 , então uma parametrização possível é:

x = x y = y z = x 2 + y 2

Assim o vetor r → é:

r → = x i → + y j → + x 2 + y 2 k →

E as derivadas parciais r → x e r → y são:

r → x = d r d x = 1 i → + x x 2 + y 2 k →

r → y = d r d y = 1 j → + y x 2 + y 2 k →

E o produto vetorial entre eles é:

r → x × r → y = i → j → k → 1 0 x x 2 + y 2 0 1 y x 2 + y 2 = - x x 2 + y 2 i → - y x 2 + y 2 j → - k →

Aqui só aplicamos o determinante.

Aplicando o módulo, vamos ter:

r → x × r → y = - x x 2 + y 2 2 + - x x 2 + y 2 2 + - 1 2

r → x × r → y = x 2 + y 2 x 2 + y 2 + 1

r → x × r → y = 2

Passo 4

Até aqui show galera!

Agora vamos substituir na nossa integral:

I z = ∬ S x 2 + y 2 ρ ( x , y , z ) n → d A

ρ ( x , y , z ) = 10 - x 2 + y 2

n → = r → x × r → y = 2

Vai ficar assim:

I z = ∬ S x 2 + y 2 ( 10 - x 2 + y 2 ) 2   d A

Aqui vamos usar o truque das coordenadas polares, pois vai facilitar muito nossa vida. Isso é possível porque a projeção do funil no plano x y é uma série de círculos com raios que variam entre 1 e 4 , pois 1 ≤ z ≤ 4 .

Em coordenadas polares temos que:

x = r   c o s   θ

y = r   s e n   θ

E,

1 ≤ r ≤ 4 0 ≤ θ ≤ 2 π   d A = r d r d θ

Pronto, agora é só jogar na integral! Vai ficar assim:

I z = ∬ S ( r cos ⁡ θ ) 2 + ( r   s e n   θ ) 2 ( 10 - ( r cos ⁡ θ ) 2 + ( r   s e n   θ ) 2 ) 2   d A

Sabemos da seguinte relação trigonométrica:

cos 2 ⁡ θ + s e n 2   θ = 1

Logo, simplificando nossa integral, vamos ter:

I z = ∫ 0 2 π ∫ 1 4 r 2 2 10 - r r d r d θ

I z = 2 ∫ 0 2 π ∫ 1 4 10 r 3 - r 4 d r d θ

Passo 5

Agora é só integrar.

Vamos começar integrando em d r . Vamos ter:

I z = 2 ∫ 0 2 π 10 r 4 4 - r 5 5 1 4 d θ

Substituindo os intervalos de integração, temos:

I z = 2 ∫ 0 2 π 10 ( 4 ) 4 4 - ( 4 ) 5 5 - 10 ( 1 ) 4 4 - ( 1 ) 5 5 d θ

I z = 2 ∫ 0 2 π 640 - 1024 5 - 10 4 - 1 5 d θ

I z = 2 ∫ 0 2 π 4329 10 d θ

Agora vamos integrar em d θ . Ficamos com:

I z = 4329 10 2   θ 0 2 π

Aplicando os limites de integração, temos que o momento de inercia em relação ao eixo z é:

I z = 8658 10 π 2

Ou, aproximadamente:

I z = 1,22 π × 10 3

Resposta

( a )     I z = ∬ S ( x 2 + y 2 ) ρ ( x , y , z ) d S

( b )     I z = 1,22 π × 10 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o centro de massa da superfície homogênea (densidade constante) dada: σ u , v = u ,v ,u 2 + v 2 , u 2 + v 2 ≤ 1 .
Calcule o momento de inércia da superfície homogênea, de massa M , de equação x 2 + y 2 = R 2( R0 ) , com 0 ≤ z ≤ 1 em torno do eixo O z .
Calcule o momento de inércia da superfície homogênea, de massa M , de equação z = x 2 + y 2 ,x 2 + y 2 ≤ R 2( R0 ) em torno do eixo O z .
Calcule o centro de massa da superfície homogênea (densidade constante) dada: b )σ é a parte da superfície cônica z 2 = x 2 + y 2 compreendida entre os planos z = 1 e z = 2 .
Calcule o momento de inércia da superfície esférica de raio R , homogênea, de massa M , em torno de qualquer diâmetro. (Tal superfície deve ser imaginada como um corpo delgado e homogêneo)